
【题目】如图,正方形ABCD的边长为2,E是BC的中点,以点A为中心,把△ABE逆时针旋转90°,设点E的对应点为F. 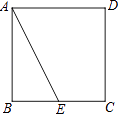
(1)画出旋转后的三角形.
(2)在(1)的条件下,
①求EF的长;
②求点E经过的路径弧EF的长.
【答案】
(1)解:如图1所示.△ADF为所求
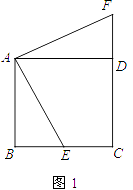
(2)解:①如图2,依题意,AE=AF,∠EAF=90°.
在Rt△ABE中,
∵AB=2,BE= ![]() BC=1,
BC=1,
∴AE= ![]() .
.
在Rt△AEF中,
EF= ![]() =
= ![]() =
= ![]() ;
;
②∵∠EAF=90°,AE=AF= ![]() ,
,
∴l= ![]() =
= ![]() π,
π,
∴弧EF的长为 ![]() π
π
【解析】(1)根据图形旋转的性质画出旋转后的图形即可;(2)①先根据勾股定理求出AE的长,由图形旋转的性质得出AF的长,根据勾股定理即可得出EF的长;②直接根据弧长公式即可得出结论.
【考点精析】通过灵活运用勾股定理的概念和弧长计算公式,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的即可以解答此题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系.直至水温降至20℃时自动开机加热,重复上述自动程序.若在水温为20℃时,接通电源后,水温y(℃)和时间x(min)的关系如图,
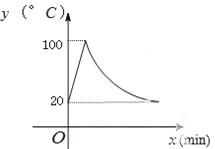
(1) 分别求出直线及双曲线的解析式.
(2) 学生在每次温度升降过程中能喝到50℃以上水的时间有多长?
(3) 若某天上午六点饮水机自动接通电源,问学生上午第一节下课时(8:15)能喝到超过50℃的水吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
(1)写出数轴上点B所表示的数 ;
(2)点P所表示的数 ;(用含t的代数式表示);
(3)M是AP的中点,N为PB的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,说明理由;若不变,请你画出图形,并求出线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.
![]()
(1)请写出与A,B两点距离相等的点M所对应的数 .
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,x秒后两只电子蚂蚁在数轴上的C点相遇,请列方程求出x,并指出点C表示的数.
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,y秒后两只电子蚂蚁在数轴上的D点相遇,请列方程求出y并指出点D表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+2+22+23+24+25+26的值时,小明发现:从第二个加数起每一个加数都是前一个加数的2倍,于是他设:S=1+2+22+23+24+25+26①然后在①式的两边都乘以2,得:2S=2+22+23+24+25+26+27 ②;②﹣①得2S﹣S=27﹣1,S=27﹣1,即1+2+22+23+24+25+26=27﹣1.
(1)求1+3+32+33+34+35+36的值;
(2)求1+a+a2+a3+…+a2013(a≠0且a≠1)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平整的地面上,由若干个完全相同的棱长为 10 cm 的小正方体堆成一个几何体,如图 所示.
(1)这个几何体由多少个小正方体组成?请画出这个几何体的三视图.
(2)如果在这个几何体的表面(不包括底面)喷上黄色的漆,则在所有的小正方体中,有多少个只有一个面是黄色?有多少个只有两个面是黄色?有多少个只有三个面是黄色?
(3)假设现在你手里还有一些相同的小正方体,保持这个几何体的主视图、俯视图形状 不变,最多可以再添加几个小正方体?这时如果要重新给这个几何体表面(不包括底面) 喷上红色的漆,需要喷漆的面积比原几何体增加了还是减少了?增加或减少的面积是 多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三条角平分线相交于点I,过点I作DI⊥IC,交AC于点D.
(1)如图①,求证:∠AIB=∠ADI;
(2)如图②,延长BI,交外角∠ACE的平分线于点F.
①判断DI与CF的位置关系,并说明理由;
②若∠BAC=70°,求∠F的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司向甲、乙两所中学送水,每次送往甲中学7600升,乙中学4000升.已知人均送水量相同,甲中学师生人数是乙中学的2倍少20人.
(1)求这两所中学师生人数分别是多少;
(2)若送瓶装水,价格为1元/升;若用消防车送饮用水,不需购买,但需配送水塔,容量500升的水塔售价为520元/个,其他费用不计.请问这次乙中学用瓶装水花费少还是饮用消防车送水花费少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着手机的普及,微信![]() 一种聊天软件
一种聊天软件![]() 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况![]() 超额记为正,不足记为负
超额记为正,不足记为负![]() 单位:斤
单位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com