
ЎѕМвДїЎїФЪЖЅХыµДµШГжЙПЈ¬УЙИфёЙёцНкИ«ПаН¬µДАві¤ОЄ 10 cm µДРЎХэ·ЅМе¶СіЙТ»ёцјёєОМеЈ¬ИзНј ЛщКѕ.
(1)ХвёцјёєОМеУЙ¶аЙЩёцРЎХэ·ЅМеЧйіЙ?Зл»іцХвёцјёєОМеµДИэКУНј.
(2)Из№ыФЪХвёцјёєОМеµД±нГж(І»°ьАЁµЧГж)ЕзЙП»ЖЙ«µДЖбЈ¬ФтФЪЛщУРµДРЎХэ·ЅМеЦРЈ¬УР¶аЙЩёцЦ»УРТ»ёцГжКЗ»ЖЙ«?УР¶аЙЩёцЦ»УРБЅёцГжКЗ»ЖЙ«?УР¶аЙЩёцЦ»УРИэёцГжКЗ»ЖЙ«?
(3)јЩЙиПЦФЪДгКЦАп»№УРТ»Р©ПаН¬µДРЎХэ·ЅМеЈ¬±ЈіЦХвёцјёєОМеµДЦчКУНјЎўё©КУНјРОЧґ І»±дЈ¬Чо¶аїЙТФФЩМнјУјёёцРЎХэ·ЅМе?ХвК±Из№ыТЄЦШРВёшХвёцјёєОМе±нГж(І»°ьАЁµЧГж) ЕзЙПємЙ«µДЖбЈ¬РиТЄЕзЖбµДГж»э±ИФјёєОМеФцјУБЛ»№КЗјхЙЩБЛ?ФцјУ»тјхЙЩµДГж»эКЗ ¶аЙЩ?

Ўѕґр°ёЎїјыЅвОц
ЎѕЅвОцЎї
ЈЁ1Ј©№ЫІмЛщёшµДјёєОМеїЙµГЈ¬ґУЧуНщУТИэБРРЎХэ·ЅМеµДёцКэТАґООЄЈє6Ј¬2Ј¬2Ј¬ПајУјґїЙЈ»ёщѕЭИэКУНјµД¶ЁТе»іцНјРОјґїЙЈ»ЈЁ2Ј©Ц»УРТ»ёцГжКЗ»ЖЙ«µДУ¦ёГКЗµЪТ»БРХэ·ЅМеЦРЧоµЧІгЦРјдДЗёцЈ»УР2ёцГжКЗ»ЖЙ«µДУ¦КЗµЪТ»БРЧоµЧІгЧоєуГжДЗёцєНµЪ¶юБРЧоєуГжДЗёцЈ»Ц»УРИэёцГжКЗ»ЖЙ«µДУ¦КЗµЪТ»БРµЪ¶юІгЧоєуГжµДДЗёцЈ¬µЪ¶юБРЧоЗ°ГжДЗёцЈ¬µЪИэБРЧоµЧІгДЗёцЈ»ЈЁ3Ј©±ЈіЦЦчКУНјєНё©КУНјІ»±дЈ¬їЙНщµЪТ»БРЗ°ГжµДјёєОМеЙП·Е2ёцРЎХэ·ЅМеЈ¬ЦРјдµДјёєОМеЙП·Е1ёцРЎХэ·ЅМеЈ¬УЙФјёєОМеРиЕз32ёцГжЈ¬РВјёєОМеРиЕз38ёцГжјЖЛгјґїЙЅвґрЈ®
ЈЁ1Ј©10Ј¬ХвёцјёєОМеµДИэКУНјИзНјЛщКѕЈє
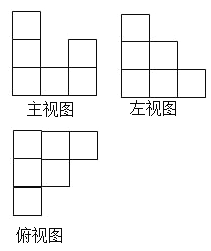 Ј»
Ј»
ЈЁ2Ј©Ц»УРТ»ёцГжКЗ»ЖЙ«µДУ¦ёГКЗµЪТ»БРХэ·ЅМеЦРЧоµЧІгЦРјдДЗёцЈ¬№І1ёцЈ»УР2ёцГжКЗ»ЖЙ«µДУ¦КЗµЪТ»БРЧоµЧІгЧоєуГжДЗёцєНµЪ¶юБРЧоєуГжДЗёцЈ¬№І2ёцЈ»Ц»УРИэёцГжКЗ»ЖЙ«µДУ¦КЗµЪТ»БРµЪ¶юІгЧоєуГжµДДЗёцЈ¬µЪ¶юБРЧоЗ°ГжДЗёцЈ¬µЪИэБРЧоµЧІгДЗёцЈ¬№І3ёцЈ»
ЈЁ3Ј©Чо¶аїЙТФФЩМнјУ3ёцРЎХэ·ЅМеЈ¬ФјёєОМеРиЕз32ёцГжЈ¬РВјёєОМеРиЕз38ёцГжЈ¬ЛщТФРиЕзЖбµДГж»эФцјУБЛЈ¬ФцјУБЛ6ЎБ10ЎБ10=600ЈЁcm2Ј©Ј®


 ФД¶БїміµПµБРґр°ё
ФД¶БїміµПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОЄ·бё»С§ЙъµДїОУа»о¶ЇЈ¬МХТ±С§ЙъµДЗйИ¤єН°®єГЈ¬ДіРЈїЄХ№БЛС§ЙъЙзНЕ»о¶ЇЈ¬ОЄБЛЅвС§ЙъёчАа»о¶ЇµДІОјУЗйїцЈ¬ёГРЈ¶ФЖЯДкј¶С§ЙъЙзНЕ»о¶ЇЅшРРБЛійСщµчІйЈ¬ЦЖЧчіцИзПВµДНіјЖНјЈє
ёщѕЭЙПКцНіјЖНјЈ¬НкіЙТФПВОКМвЈє
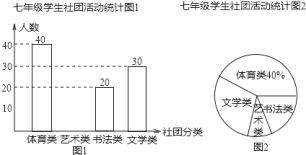
ёГРЈІОјУТХКхАаµДЙзНЕС§ЙъЦРЈ¬Е®ЙъИЛКэКЗДРЙъИЛКэµД![]() ±¶Ј¬ПЦёГРЈ№ІУРС§Йъ
±¶Ј¬ПЦёГРЈ№ІУРС§Йъ![]() ГыЈ¬Зл№АЛгёГРЈІОјУТХКхАаЙзНЕЦРЕ®ЙъУР________ИЛЈ®
ГыЈ¬Зл№АЛгёГРЈІОјУТХКхАаЙзНЕЦРЕ®ЙъУР________ИЛЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїПВ±нёшіцБЛДі°а6ГыН¬С§µДЙнёЯЗйїц(µҐО»Јєcm).
С§Йъ | A | B | C | D | E | F | |
ЙнёЯ(µҐО»Јєcm) | 165 | ____ | 166 | ____ | ____ | 172 | |
ЙнёЯУл°ај¶ЖЅ | ѕщЙнёЯµДІоЦµ) | Ј1 | Ј«2 | ____ | Ј3 | Ј«4 | ____ |
(1)НкіЙ±нЦРїХµДІї·ЦЈ»
(2)ЛыГЗ6ИЛЦРЧоёЯЙнёЯ±ИЧо°«ЙнёЯёЯ¶аЙЩЈї
(3)Из№ыЙнёЯґпµЅ»ті¬№эЖЅѕщЙнёЯК±ЅРґп±кЙнёЯЈ¬ДЗГґХв6ГыН¬С§ЙнёЯµДґп±кВККЗ¶аЙЩЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЕЧОпПЯy=ax2+bx+cЙПІї·ЦµгµДєбЧш±кxЈ¬ЧЭЧш±кyµД¶ФУ¦ЦµИз±нЈє
x | Ў | ©Ѓ2 | ©Ѓ1 | 0 | 1 | 2 | Ў |
y | Ў | 0 | 4 | 6 | 6 | 4 | Ў |
ґУ±нїЙЦЄЈ¬
ўЩЕЧОпПЯУлxЦбµДЅ»µгОЄЈ»
ўЪЕЧОпПЯµД¶ФіЖЦбКЗЈ»
ўЫєЇКэy=ax2+bx+cµДЧоґуЦµОЄЈ»
ўЬx Ј¬ yЛжxФцґу¶шФцґуЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬Хэ·ЅРОABCDµД±Яі¤ОЄ2Ј¬EКЗBCµДЦРµгЈ¬ТФµгAОЄЦРРДЈ¬°СЎчABEДжК±ХлРэЧЄ90ЎгЈ¬ЙиµгEµД¶ФУ¦µгОЄFЈ® 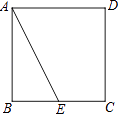
ЈЁ1Ј©»іцРэЧЄєуµДИэЅЗРОЈ®
ЈЁ2Ј©ФЪЈЁ1Ј©µДМхјюПВЈ¬
ўЩЗуEFµДі¤Ј»
ўЪЗуµгEѕ№эµДВ·ѕ¶»ЎEFµДі¤Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЈєИзНјЈ¬ФЪЎчABCЦРЈ¬DКЗBAСУі¤ПЯЙПТ»µгЈ¬AEКЗЎПDACµДЖЅ·ЦПЯЈ¬PКЗAEЙПµДТ»µгЈЁµгPІ»УлµгAЦШєПЈ©Ј¬Б¬ЅУPBЈ¬PCЈ®НЁ№э№ЫІмЈ¬ІвБїЈ¬ІВПлPB+PCУлAB+ACЦ®јдµДґуРЎ№ШПµЈ¬ІўјУТФЦ¤ГчЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЎчABCЦРЈ¬AB=ACЈ¬ЎПA=36ЎгЈ¬BDЎўCE·Ц±рКЗЎПABCЎўЎПBCDµДЅЗЖЅ·ЦПЯЈ¬ФтНјЦРµДµИСьИэЅЗРОУРЈЁЎЎЎЎЈ©

A. 5ёц B. 4ёц C. 3ёц D. 2ёц
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ЎчABCЦРЈ¬DКЗBCµДЦРµгЈ¬№эDµгµДЦ±ПЯGFЅ»ACУЪFЈ¬Ѕ»ACµДЖЅРРПЯBGУЪGµгЈ¬DEЎНDFЈ¬Ѕ»ABУЪµгEЈ¬Б¬ЅбEGЎўEFЈ®

ЈЁ1Ј©ЗуЦ¤ЈєBGЈЅCFЈ®
ЈЁ2Ј©ЗлДгЕР¶ПBE+CFУлEFµДґуРЎ№ШПµЈ¬ІўЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї(1)ИзНјўЩЈ¬RtЎчABCЦРЈ¬ЎПC=90ЎгЈ¬AC=3,BC=4.µгDКЗAB±ЯЙПИОТвТ»µгЈ¬ФтCDµДЧоРЎЦµОЄ ЎЈ
ЈЁ2Ј©ИзНјўЪЈ¬ФЪѕШРОABCDЦРЈ¬AB=3,BC=4.µгMЎўN·Ц±рФЪBDЎўBCЙПЎЈЗуCM+MNµДЧоРЎЦµЈ®
ЈЁ3Ј©ИзНјўЫЈ¬ФЪѕШРОABCDЦРЈ¬AB=3,BC=4.µгEКЗAB±ЯЙПµДТ»µгЈ¬ЗТAE=2Ј¬µгFКЗBC±ЯЙПµДИОТвТ»µгЎЈ°СЎчBEFСШEF·ХЫЈ¬µгB¶ФУ¦µгG,Б¬ЅУAGЎўCG.ЛД±ЯРОAGCDµДГж»эµДЧоРЎЦµКЗ ЎЈ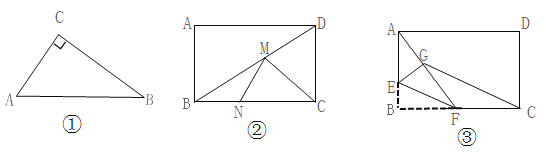
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com