
【题目】已知,如图,在△ABC中,AB=AC=20cm,BD⊥AC于D,且BD=16cm.点M从点A出发,沿AC方向匀速运动,速度为4cm/s;同时点P由B点出发,沿BA方向匀速运动,速度为lcm/s,过点P的动直线PQ∥AC,交BC于点Q,连结PM,设运动时间为t(s)(0<t<5),解答下列问题:
(1)线段AD=___cm;
(2)求证:PB=PQ;
(3)当t为何值时,以P、Q、D、M为顶点的四边形为平行四边形.

【答案】(1)AD=12cm;(2)证明见解析;(3)t=![]() s或4s
s或4s
【解析】
(1)由勾股定理求出AD即可;
(2)由等腰三角形的性质和平行线的性质得出∠PBQ=∠PQB,再由等腰三角形的判定定理即可得出结论;
(3)分两种情况:①当点M在点D的上方时,根据题意得:PQ=BP=t,AM=4t,AD=12,得出MD=AD-AM=12-4t,由PQ∥MD,当PQ=MD时,四边形PQDM是平行四边形,得出方程,解方程即可;
②当点M在点D的下方时,根据题意得:PQ=BP=t,AM=4t,AD=12,得出MD=AM-AD=4t-12,由PQ∥MD,当PQ=MD时,四边形PQDM是平行四边形,得出方程,解方程即可.
(1)解:∵BD⊥AC,
∴∠ADB=90°,
∴AD=![]() ,
,
故答案为:12;
(2)证明:∵AB=AC,
∴∠ABC=∠C,即∠PBQ=∠C,
∵PQ∥AC,
∴∠PQB=∠C,
∴∠PBQ=∠PQB,
∴PB=PQ;
(3)分两种情况:
①当点M在点D的上方时,如图所示
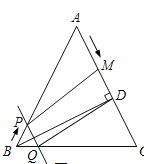
根据题意得:PQ=BP=t,AM=4t,AD=12,
∴MD=AD-AM=12-4t,
∵PQ∥AC,
∴PQ∥MD,
当PQ=MD时,四边形PQDM是平行四边形,
∴t=12-4t,
解得:t=![]() (s);
(s);
②当点M在点D的下方时,如图所示:
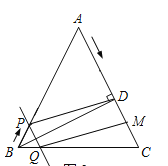
根据题意得:PQ=BP=t,AM=4t,AD=12,
∴MD=AM-AD=4t-12,
∵PQ∥AC,
∴PQ∥MD,
当PQ=MD时,四边形PQDM是平行四边形,
∴t=4t-12,
解得:t=4(s);
综上所述,当t=![]() s或t=4s时,以P、Q、D、M为顶点的四边形为平行四边形;
s或t=4s时,以P、Q、D、M为顶点的四边形为平行四边形;
故答案为:![]() s或4s.
s或4s.


科目:初中数学 来源: 题型:
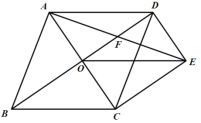
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE//AC,且DE:AC=1:2,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
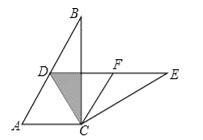
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按照顺时针方向旋转m度后得到△DEC,点D刚好落在AB边上.
(1)求m的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD为∠BAC的平分线,BM⊥AD,垂足为M,且AB=5,BM=2,AC=9,则∠ABC与∠C的关系为( )

A.∠ABC=2∠CB.∠ABC=![]() ∠CC.
∠CC.![]() ∠ABC=∠CD.∠ABC=3∠C
∠ABC=∠CD.∠ABC=3∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC与BD相交于点O,∠AOB=60°,BD=4,将△ABC沿直线AC翻折后,点B落在点E处,那么S△AED=______

查看答案和解析>>
科目:初中数学 来源: 题型:
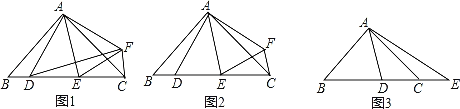
【题目】在△ABC中,AB=AC,∠BAC=2∠DAE=2α.
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“知识改变命运,科技繁荣祖国”.我市中小学每年都要举办一届科技运动会.下图为我市某校2009年参加科技运动会航模比赛(包括空模、海模、车模、建模四个类别)的参赛人数统计图:
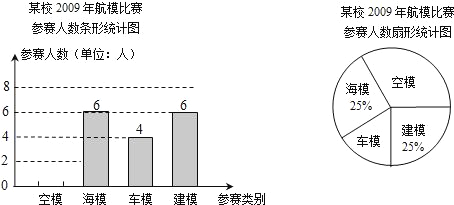
(1)该校参加车模、建模比赛的人数分别是 人和 人;
(2)该校参加航模比赛的总人数是 人,空模所在扇形的圆心角的度数是 °,并把条形统计图补充完整;(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑)
(3)从全市中小学参加航模比赛选手中随机抽取80人,其中有32人获奖.今年我市中小学参加航模比赛人数共有2485人,请你估算今年参加航模比赛的获奖人数约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择,其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调查,购买3台甲型机器和2台乙机器共需31万元,购买一台甲型机器比购买一台乙型机器多2万元.
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂购买机器的预算资金不超过34万元,那么该工厂有几种购买方案?
(3)在(2)的条件下,如果该工厂购进的6台机器的日产量能力不能低于380个,那么为了节约资金,应选择那种方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com