
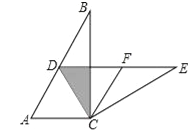
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按照顺时针方向旋转m度后得到△DEC,点D刚好落在AB边上.
(1)求m的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
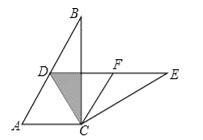
【答案】(1)60;(2)菱形.
【解析】试题分析:(1)首先证明∠A=60°,AC=DC,判断△DAC为等边三角形,得到∠ACD=60°,即可解决问题.
(2)根据题意,证明AD=AC;再证明DF=CF=AD,得到AD=DF=CF=AC,即可解决问题.
试题解析:解:(1)如图,∵∠ACB=90°,∠B=30°,∴AB=2AC,∠A=60°.
由题意得:AC=DC,∴△DAC为等边三角形,∴∠ACD=60°,∴m=60°;
(2)∵△DAC为等边三角形,∴AD=AC.∵AB=AD+BD=2AC,∴AD =BD=![]() AB,
AB,
由题意得:DE=AB,∠DCE=∠ACB=90°.
∵F是DE的中点,∴DF=CF=![]() DE=
DE=![]() AB,∴AD=DF=CF=AC,∴四边形ACFD为菱形.
AB,∴AD=DF=CF=AC,∴四边形ACFD为菱形.


科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中有3个分别标有数字-1、1、2的小球,它们除标的数字不同外无其他区别.
(1)随机地从口袋中取出一小球,求取出的小球上标的数字为负数的概率;
(2)随机地从口袋中取出一小球,放回后再取出第二个小球,求两次取出的数字的和等于0的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算F,规定:F(x,y)=ax+by(其中a,b均为非零常数).例如:F(3,4)=3a+4b.
(1)已知F(1,﹣1)=﹣1,F(2,0)=4.
①求a,b的值;
②已知关于p的不等式组![]() ,求p的取值范围;
,求p的取值范围;
(2)若运算F满足![]() ,请你直接写出F(m,m)的取值范围(用含m的代数式表示,这里m为常数且m>0).
,请你直接写出F(m,m)的取值范围(用含m的代数式表示,这里m为常数且m>0).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )

A.内部 B.外部 C.边上 D.以上都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
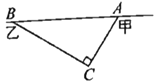
【题目】在甲村至乙村的公路上有一块山地正在开发,现有一![]() 处需要爆破.已知点
处需要爆破.已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为300米,与公路上的另一停靠站
的距离为300米,与公路上的另一停靠站![]() 的距离为400米,且
的距离为400米,且![]() ,如图所示为了安全起见,爆破点
,如图所示为了安全起见,爆破点![]() 周围半径250米范围内不得进入,问在进行爆破时,公路
周围半径250米范围内不得进入,问在进行爆破时,公路![]() 段是否因为有危险而需要暂时封锁?请说明理由.
段是否因为有危险而需要暂时封锁?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2﹣4x+3与x轴交于A,B两点,其顶点为C.
(1)对于任意实数m,点M(m,﹣2)是否在该抛物线上?请说明理由;
(2)求证:△ABC是等腰直角三角形;
(3)若点D在x轴上,则在抛物线上是否存在点P,使得PD∥BC,且PD=BC?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.2万元,乙队每天的施工费用为5.8万元.工程预算的施工费用为501万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,AB=AC=20cm,BD⊥AC于D,且BD=16cm.点M从点A出发,沿AC方向匀速运动,速度为4cm/s;同时点P由B点出发,沿BA方向匀速运动,速度为lcm/s,过点P的动直线PQ∥AC,交BC于点Q,连结PM,设运动时间为t(s)(0<t<5),解答下列问题:
(1)线段AD=___cm;
(2)求证:PB=PQ;
(3)当t为何值时,以P、Q、D、M为顶点的四边形为平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是CD边上一动点,DF⊥BE交BE的延长线于F.

(1)如图(1),若BE平分∠DBC时,
①直接写出∠FDC的度数;
②延长DF交BC的延长线于点H,补全图形,探究BE与DF的数量关系,并证明你的结论;
(2)如图(2),过点C作CG⊥BE于点G,猜想线段BF,CG,DF之间的数量关系,并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com