
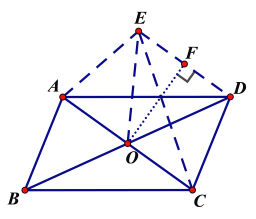
【题目】如图,在平行四边形ABCD中,AC与BD相交于点O,∠AOB=60°,BD=4,将△ABC沿直线AC翻折后,点B落在点E处,那么S△AED=______

【答案】![]()
【解析】
根据题意画出翻折后的图形,连接OE、DE,先证明△OED是等边三角形,再利用同底等高的三角形面积相等,说明S△AED=S△OED,作OF⊥ED于F,求出△OED的面积即可得出结果.
解:如图,△AEC是△ABC沿AC翻折后的图形,连接OE、DE,
∵四边形ABCD是平行四边形,
∴OB=OD=![]() BD=2,
BD=2,
∵△AEC是△ABC沿AC翻折后的图形,∠AOB=60,
∴∠AOE=60,OE=OB,
∴∠EOD=60,OE=OD,
∴△OED是等边三角形,
∴∠DEO=∠AOE=60,ED=OD=2,
∴ED∥AC,
∴S△AED=S△OED,
作OF⊥ED于F,DF=![]() ED=1,
ED=1,
∴OF=![]() =
=![]() ,
,
∴S△OED=![]() ED·DF=
ED·DF=![]()
∴S△AED=![]() .
.
故答案为:![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
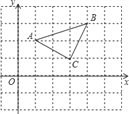
【题目】如图所示,三角形ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).
(1)三角形A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB和CD相交于点O,在∠COB的内部作射线OE.
(1)若∠AOC=36°,∠COE=90°,求∠BOE的度数;
(2)若∠COE:∠EOB:∠BOD=4:3:2,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器经营业主计划购进一批同种型号的冷风扇和普通电风扇,若购进8台冷风扇和20台普通电风扇,需要资金17400元,若购进10台冷风扇和30台普通电风扇,需要资金22500元.求冷风扇和普通电风扇每台的采购价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人再次选择自行车作为出行工具,小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题: 
(1)a= , b= , m= ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
(4)若小军的行驶速度是v米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出v的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF 过平行四边形 ABCD 对角线的交点 O,交 AD 于 E,交 BC 于 F,若平行四边形 ABCD 的周长为32,OE=2,则四边形 ABFE 的周长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一种圆环甲(如图1),它的外圆直径是8厘米,环宽1厘米。
①如果把这样的2个圆环扣在一起并拉紧(如图2),长度为 厘米;
②如果用n个这样的圆环相扣并拉紧,长度为 厘米。
(2)另一种圆环乙,像(1)中圆环甲那样相扣并拉紧,
①3个圆环乙的长度是28cm,5个圆环乙的长度是44cm,求出圆环乙的外圆直径和环宽;
②现有n(n>2)个圆环甲和n(n>2)个圆环乙,将它们像(1)中那样相扣并拉紧,长度用n的代数式表示为多少厘米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com