
【题目】某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择,其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调查,购买3台甲型机器和2台乙机器共需31万元,购买一台甲型机器比购买一台乙型机器多2万元.
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂购买机器的预算资金不超过34万元,那么该工厂有几种购买方案?
(3)在(2)的条件下,如果该工厂购进的6台机器的日产量能力不能低于380个,那么为了节约资金,应选择那种方案?
【答案】(1)甲种机器每台7万元,乙种机器每台5万元;(2)有三种购买方案:
①购买甲种机器0台,乙种机器6台,②购买甲种机器1台,乙种机器5台,③购买甲种机器2台,乙种机器4台;(3)②购买甲种机器1台,乙种机器5台该方案符合要求.
【解析】
(1)设甲种机器每台x万元,乙种机器每台y万元,列出方程组即可解决问题.
(2)设购买甲种机器a台,乙种机器(6-a)台,构建不等式解决问题.
(3)分别求出各种方案的费用,日产量能力即可解决问题.
解:(1)设甲种机器每台x万元,乙种机器每台y万元,
由题意得:![]() ,解得:
,解得:![]() ,
,
答:甲种机器每台7万元,乙种机器每台5万元;
(2)设购买甲种机器a台,乙种机器(6-a)台,
由题意7a+5(6-a)≤34,
解得a≤2,
∵a是整数,a≥0
∴a=0或1或2,
∴有三种购买方案:
①方案购买甲种机器0台,乙种机器6台,
②方案购买甲种机器1台,乙种机器5台,
③方案购买甲种机器2台,乙种机器4台;
(3)①方案费用6×5=30万元,日产量能力360个,
②方案费用7+5×5=32万元,日产量能力406个,
③方案费用为2×7+4×5=34万元,日产量能力452个,
综上所述,②方案购买甲种机器1台,乙种机器5台满足条件.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,AB=AC=20cm,BD⊥AC于D,且BD=16cm.点M从点A出发,沿AC方向匀速运动,速度为4cm/s;同时点P由B点出发,沿BA方向匀速运动,速度为lcm/s,过点P的动直线PQ∥AC,交BC于点Q,连结PM,设运动时间为t(s)(0<t<5),解答下列问题:
(1)线段AD=___cm;
(2)求证:PB=PQ;
(3)当t为何值时,以P、Q、D、M为顶点的四边形为平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是CD边上一动点,DF⊥BE交BE的延长线于F.

(1)如图(1),若BE平分∠DBC时,
①直接写出∠FDC的度数;
②延长DF交BC的延长线于点H,补全图形,探究BE与DF的数量关系,并证明你的结论;
(2)如图(2),过点C作CG⊥BE于点G,猜想线段BF,CG,DF之间的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在△ABC中,∠C=60°,∠A=40°.

(1)用尺规作图作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);
(2)求证:BD平分∠CBA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中A(a,0),B(0,b),且a,b满足![]() .
.


(1) (2)
(1)A、B坐标分别为A( ) 、B( ).
(2)P为x轴上一点,C为AB中点,∠APC=∠PBO,求AP的长.
(3)如图2,点E为第一象限一点,AE=AB,以AE为斜边构造等腰直角△AFE,连BE,连接OF并延长交BE于点G,求证:BG=EG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线PQ∥MN,点A在直线PQ上,点C、D在直线MN上,连接AC、AD,∠PAC=50°,∠ADC=30°,AE平分∠PAD,CE平分∠ACD,AE与CE相交于点E.



(1)若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置,此时A1E平分∠AA1D1,CE平分∠ACD1,A1E与CE相交于E,∠PAC=50°,∠A1D1C=30°,求∠A1EC的度数.
(2)若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置,其他条件与(1)相同,求此时∠A1EC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形。
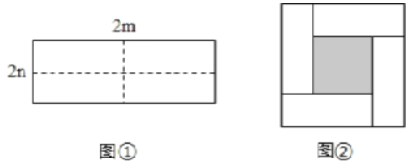
(1)用两种不同的方法表示图②中小正方形(阴影部分)的面积:
方法一:![]() ;
;
方法二:![]() .
.
(2)(m+n)![]() ,(mn)
,(mn) ![]() ,mn这三个代数式之间的等量关系为___
,mn这三个代数式之间的等量关系为___
(3)应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求xy的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果生产基地,某天安排30名工人采摘枇杷或草莓(每名工人只能做其中一项工作),并且每人每天摘0.4吨枇杷或0.3吨草莓,当天的枇杷售价每吨2000元,草莓售价每吨3000元,设安排其中x名工人采摘枇杷,两种水果当天全部售出,销售总额达y元.
(1)求y与x之间的函数关系式;
(2)若要求当天采摘枇杷的数量不少于草莓的数量,求销售总额的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com