Question

【题目】如图1，在平面直角坐标系中A（a,0），B（0，b），且a,b满足.

(1) (2)

（1）A、B坐标分别为A( ) 、B( ).

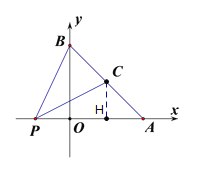
（2）P为x轴上一点，C为AB中点，∠APC=∠PBO,求AP的长.

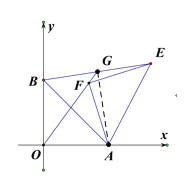
（3）如图2，点E为第一象限一点，AE=AB，以AE为斜边构造等腰直角△AFE，连BE，连接OF并延长交BE于点G，求证：BG=EG.

Answer 1

【答案】（1）A（4，0），B（0，4）；（2）6；（3）见解析.

【解析】

（1）根据解出a，b的值，即可求出A，B的坐标；

（2）作CH⊥AP于点H，由△AOB为等腰直角三角形，可证明∠PBC=∠PCB，从而证明△PBO≌△CPH，即可求出AP长；

（3）连接AG，根据题意证明△AOB≌△AFE，再根据角度转换得到∠BGO，∠AGO的度数，即可证明∠AGB=90°，即可证明BG=EG.

（1）由得：a=b=4，

则点A坐标为（4，0），点B坐标为（0，4）；

（2）作CH⊥AP于点H，

由（1）知△AOB为等腰直角三角形，

∴∠OBA=∠OAB=45°，

∵∠APC=∠PBO，

∴∠PCB=∠APC+∠CAP，∠PBC=∠PBO+∠OBA，

∴∠PBC=∠PCB，

∴PB=PC，

在△PBO和△CPH中

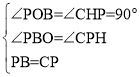
∴△PBO≌△CPH（AAS），

∵C为AB中点，

∴CH=2，

∴PO=CH=2，

∴AP=OA+OP=4+2=6；

（3）连接AG，

∵△AFE为等腰直角三角形，AE=AB，

在△AOB和△AFE中

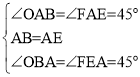
∴△AOB≌△AFE（ASA），

∴∠OAF=∠BAE，

∴∠FOA=∠EBA，

∴∠BGO=∠OAB=45°，

∴∠BOF=∠BAG，

∴∠AGO=∠OBA=45°，

∴∠BGA=90°，

∵△ABE为等腰三角形，

根据等腰三角形的三线合一知G为BE中点，

∴BG=EG.