
【题目】如图1,已知直线PQ∥MN,点A在直线PQ上,点C、D在直线MN上,连接AC、AD,∠PAC=50°,∠ADC=30°,AE平分∠PAD,CE平分∠ACD,AE与CE相交于点E.



(1)若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置,此时A1E平分∠AA1D1,CE平分∠ACD1,A1E与CE相交于E,∠PAC=50°,∠A1D1C=30°,求∠A1EC的度数.
(2)若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置,其他条件与(1)相同,求此时∠A1EC的度数.
【答案】(1)130°;(2)40°.
【解析】
(1)直接利用角平分线的性质结合平行线的性质得出∠CAE以及∠ECA的度数,进而得出答案;
(2)直接利用角平分线的性质结合平行线的性质得出∠1和∠2的度数,进而得出答案.
解:(1)如图所示:
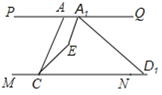
∵∠A1D1C=30°,线段AD沿MN向右平移到A1D1,PQ∥MN,
∴∠QA1D1=30°,
∴∠PA1D1=150°,
∵A1E平分∠AA1D1,
∴∠PA1E=∠EA1D1=75°,
∵∠PAC=50°,PQ∥MN,
∴∠CAQ=130°,∠ACN=50°,
∵CE平分∠ACD1,
∴∠ACE=25°,
∴∠A1EC =360°-25°-130°-75°=130°;
(2)如图所示:

过点E作FE∥PQ,
∵∠A1D1C=30°,线段AD沿MN向左平移到A1D1,PQ∥MN,
∴∠QA1D1=30°,
∵A1E平分∠AA1D1,
∴∠QA1E=∠2=15°,
∵∠PAC=50°,PQ∥MN,
∴∠ACN=50°,
∵CE平分∠ACD1,
∴∠ACE=∠ECN=∠1=25°,
∴∠A1EC =∠1+∠2=15°+25°=40°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
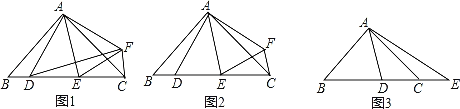
【题目】在△ABC中,AB=AC,∠BAC=2∠DAE=2α.
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中
(1)求作:△ABC的内切圆⊙O(要求尺规作图,保留作图痕迹,不必写作法)
(2)综合应用:在你所作的圆中,若∠AOB=140°,求∠C的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择,其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调查,购买3台甲型机器和2台乙机器共需31万元,购买一台甲型机器比购买一台乙型机器多2万元.
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂购买机器的预算资金不超过34万元,那么该工厂有几种购买方案?
(3)在(2)的条件下,如果该工厂购进的6台机器的日产量能力不能低于380个,那么为了节约资金,应选择那种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市中小学全面开展“阳光体育”活动,某校在大课间中开设了A(体操)、B(乒乓球)、C(毽球)、D(跳绳)四项活动.为了解学生最喜欢哪一项活动,随机抽了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:

(1)这次被调查的学生共有 人;
(2)请将统计图2补充完整;
(3)统计图1中B项目对应的扇形的圆心角是 度;
(4)已知该校共有学生2500人,根据调查结果估计该校喜欢体操的学生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x与反比例函数y=![]() (k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图象上任意一点(不与点A重合),BC⊥x轴于点C.
(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图象上任意一点(不与点A重合),BC⊥x轴于点C.
(1)求k的值;
(2)求△OBC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]() .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,
求两次摸 出都是红球的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,完成下列各题:
,完成下列各题:
(1)将函数关系式用配方法化为 y=a(x+h)2+k形式,并写出它的顶点坐标、对称轴.
(2)若它的图象与x轴交于A、B两点,顶点为C,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com