
【题目】已知二次函数![]() ,完成下列各题:
,完成下列各题:
(1)将函数关系式用配方法化为 y=a(x+h)2+k形式,并写出它的顶点坐标、对称轴.
(2)若它的图象与x轴交于A、B两点,顶点为C,求△ABC的面积.
【答案】(1) 抛物线的顶点坐标为(2,4),对称轴为直线x=2.(2) ![]() .
.
【解析】试题分析:
(1)用“配方法”把二次函数![]() 化为顶点式:y=a(x+h)2+k的形式即可得到本题答案;
化为顶点式:y=a(x+h)2+k的形式即可得到本题答案;
(2)由(1)中结果可得点C的坐标,解方程![]() 可求得A、B的坐标,由此即可求出△ABC的面积.
可求得A、B的坐标,由此即可求出△ABC的面积.
试题解析:
(1)∵y=-2x2+8x-4
=-2(x2-4x)-4
=-2(x2-4x+4-4)-4
=-2(x-2)2+4.
∴抛物线![]() 的顶点坐标为(2,4),对称轴为直线x=2.
的顶点坐标为(2,4),对称轴为直线x=2.
(2)令y=0可得:-2(x-2)2+4=0,即:(x-2)2=2,
解得:x-2=![]() ,即:x1=
,即:x1=![]() ,x2=
,x2=![]() .
.
∴与x轴的交点坐标为A(![]() ,0),B(
,0),B(![]() ,0).
,0).
又∵顶点C的坐标为(2,4),
∴S△ABC=![]() ×[(
×[(![]() )-(
)-(![]() )] ×4=
)] ×4=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知直线PQ∥MN,点A在直线PQ上,点C、D在直线MN上,连接AC、AD,∠PAC=50°,∠ADC=30°,AE平分∠PAD,CE平分∠ACD,AE与CE相交于点E.



(1)若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置,此时A1E平分∠AA1D1,CE平分∠ACD1,A1E与CE相交于E,∠PAC=50°,∠A1D1C=30°,求∠A1EC的度数.
(2)若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置,其他条件与(1)相同,求此时∠A1EC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2010年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2012年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2012年底共建设了多少万平方米廉租房.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丹尼斯超市举行有奖促销活动:顾客凡一次性购买满![]() 元者即可获得一次摇奖机会.摇奖机是一个圆形转盘,被等分成
元者即可获得一次摇奖机会.摇奖机是一个圆形转盘,被等分成![]() 个扇形,如果转盘停止后,指针正好对准红黄或蓝色区域,顾客就可以分别获得一、二、三等奖奖金依次为
个扇形,如果转盘停止后,指针正好对准红黄或蓝色区域,顾客就可以分别获得一、二、三等奖奖金依次为![]() 元、
元、![]() 元、
元、![]() 元一次性购物满
元一次性购物满![]() 元者,如果不摇奖可返还奖金
元者,如果不摇奖可返还奖金![]() 元.
元.

(1)摇奖一次,获一等奖、二等奖、三等奖的概率分别是多少?
(2)小李一次性购物满![]() 元他是参与摇奖划算,还是领
元他是参与摇奖划算,还是领![]() 元现金划算?请你帮他算算
元现金划算?请你帮他算算
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果生产基地,某天安排30名工人采摘枇杷或草莓(每名工人只能做其中一项工作),并且每人每天摘0.4吨枇杷或0.3吨草莓,当天的枇杷售价每吨2000元,草莓售价每吨3000元,设安排其中x名工人采摘枇杷,两种水果当天全部售出,销售总额达y元.
(1)求y与x之间的函数关系式;
(2)若要求当天采摘枇杷的数量不少于草莓的数量,求销售总额的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若(7﹣x)(x﹣4)=1,求(7﹣x)2+(x﹣4)2的值;
(2)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=5,两正方形的面积和S1+S2=17,求图中阴影部分面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
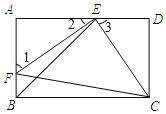
【题目】如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
(1)求证:△AEF≌△DCE;
(2)若CD=1,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
(1)求证:四边形PMAN是正方形;
(2)求证:EM=BN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上的一点,DA与⊙O相切于点A,DA=DC=![]() .
.

(1)求证:DC是⊙O的切线;
(2)若∠CAB=30°,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com