
【题目】图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形。
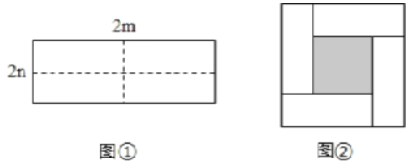
(1)用两种不同的方法表示图②中小正方形(阴影部分)的面积:
方法一:![]() ;
;
方法二:![]() .
.
(2)(m+n)![]() ,(mn)
,(mn) ![]() ,mn这三个代数式之间的等量关系为___
,mn这三个代数式之间的等量关系为___
(3)应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求xy的值.
【答案】(1)(m+n)![]() 4mn,(mn)
4mn,(mn)![]() ;(2)(m+n)
;(2)(m+n)![]() 4mn=(mn)
4mn=(mn)![]() ;(3)±5.
;(3)±5.
【解析】
(1)观察图形可确定:方法一,大正方形的面积为(m+n)![]() ,四个小长方形的面积为4mn,中间阴影部分的面积为S=(m+n)
,四个小长方形的面积为4mn,中间阴影部分的面积为S=(m+n)![]() -4mn;
-4mn;
方法二,图2中阴影部分为正方形,其边长为m-n,所以其面积为(m-n)![]() .
.
(2)观察图形可确定,大正方形的面积减去四个小长方形的面积等于中间阴影部分的面积,即(m+n)![]() -4mn=(m-n)
-4mn=(m-n)![]() .
.
(3)根据(2)的关系式代入计算即可求解.
(1)方法一:S小正方形=(m+n) ![]() 4mn.
4mn.
方法二:S小正方形=(mn) ![]() .
.
(2)(m+n)![]() ,(mn)
,(mn)![]() ,mn这三个代数式之间的等量关系为(m+n)
,mn这三个代数式之间的等量关系为(m+n)![]() 4mn=(mn)
4mn=(mn)![]() .
.
(3)∵x+y=9,xy=14,
∴xy=![]() =±5.
=±5.
故答案为:(m+n)![]() 4mn,(mn)
4mn,(mn) ![]() ;(m+n)
;(m+n)![]() 4mn=(mn)
4mn=(mn)![]() ,±5.
,±5.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】“知识改变命运,科技繁荣祖国”.我市中小学每年都要举办一届科技运动会.下图为我市某校2009年参加科技运动会航模比赛(包括空模、海模、车模、建模四个类别)的参赛人数统计图:
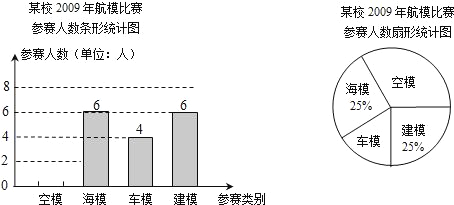
(1)该校参加车模、建模比赛的人数分别是 人和 人;
(2)该校参加航模比赛的总人数是 人,空模所在扇形的圆心角的度数是 °,并把条形统计图补充完整;(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑)
(3)从全市中小学参加航模比赛选手中随机抽取80人,其中有32人获奖.今年我市中小学参加航模比赛人数共有2485人,请你估算今年参加航模比赛的获奖人数约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区环保部门为了提高宣传垃圾分类的实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,进行整理后,绘制了如下两幅不完整的统计图:
根据统计图解答下列问题:
(1)求抽样调查的生活垃圾的总吨数;
(2)求扇形统计图中,“D”部分所对应的圆心角的度数,并将条形统计图补充完整;
(3)调查发现,在可回收物中废纸垃圾约占![]() ,每回收 1 吨废纸可再造 0.85 吨的再生纸,假设该城市每月生产的生活垃圾为10000 吨,且全部分类处理,那么每月回收的废纸可制成再生纸多少吨?
,每回收 1 吨废纸可再造 0.85 吨的再生纸,假设该城市每月生产的生活垃圾为10000 吨,且全部分类处理,那么每月回收的废纸可制成再生纸多少吨?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择,其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调查,购买3台甲型机器和2台乙机器共需31万元,购买一台甲型机器比购买一台乙型机器多2万元.
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂购买机器的预算资金不超过34万元,那么该工厂有几种购买方案?
(3)在(2)的条件下,如果该工厂购进的6台机器的日产量能力不能低于380个,那么为了节约资金,应选择那种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+5的图象与反比例函数![]() (k≠0)在第一象限的图象交于A(1,n)和B两点.
(k≠0)在第一象限的图象交于A(1,n)和B两点.

(1)求反比例函数的解析式及点B坐标;
(2)在第一象限内,当一次函数y=-x+5的值大于反比例函数![]() (k≠0)的值时,写出自变量x的取值范围.
(k≠0)的值时,写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x与反比例函数y=![]() (k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图象上任意一点(不与点A重合),BC⊥x轴于点C.
(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图象上任意一点(不与点A重合),BC⊥x轴于点C.
(1)求k的值;
(2)求△OBC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小丽想知道自家门前小河的宽度,于是她按以下办法测出了如下数据:小丽在河岸边选取点A,在点A的对岸选取一个参照点C,测得∠CAD=30°;小丽沿岸向前走30m选取点B,并测得∠CBD=60°.请根据以上数据,用你所学的数学知识,帮小丽计算小河的宽度.

查看答案和解析>>
科目:初中数学 来源: 题型:
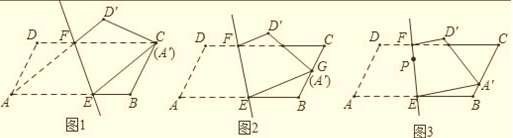
【题目】直线EF分别平行四边形ABCD边AB、 CD于点E、F,将图形沿直线EF对折,点A、D分别落在点、A',D'处,
(1) 如图1,当点A’与点C重合时,连接AF,求证:四边形AECF是菱形:
(2)若∠A=60°,AD=4, AB=8,
①如图2.当点A’与BC边的中点G重合时,求AE的长;
②如图3.当点A’落在BC边上任意点时,设点P为直线EF上的动点,请直接写出PC+PA’的最小值 ;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com