
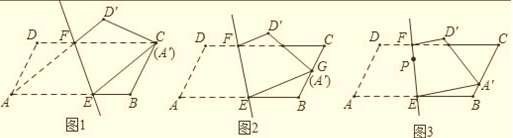
【题目】直线EF分别平行四边形ABCD边AB、 CD于点E、F,将图形沿直线EF对折,点A、D分别落在点、A',D'处,
(1) 如图1,当点A’与点C重合时,连接AF,求证:四边形AECF是菱形:
(2)若∠A=60°,AD=4, AB=8,
①如图2.当点A’与BC边的中点G重合时,求AE的长;
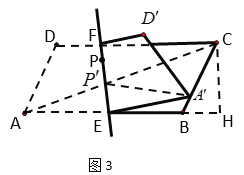
②如图3.当点A’落在BC边上任意点时,设点P为直线EF上的动点,请直接写出PC+PA’的最小值 ;
【答案】(1)见解析;(2)①AE=![]() ;②
;②![]()
【解析】
(1)先证明四边形AECF是平行四边形,再由翻折得AF=CF,则四边形AFCE是菱形;
(2)①如图2中,作![]() H⊥AB交AB的延长线于H,首先求出GH、BH,设AE=EG=x,在Rt△EGH中,根据
H⊥AB交AB的延长线于H,首先求出GH、BH,设AE=EG=x,在Rt△EGH中,根据![]() 构建方程即可解决问题;
构建方程即可解决问题;
②如图3中,连接AC交EF于![]() ,连接
,连接![]()
![]() ,作CH⊥AB交AB的延长线于H,因为A、
,作CH⊥AB交AB的延长线于H,因为A、![]() 关于直线EF对称,推出
关于直线EF对称,推出![]()
![]() +
+![]() C=
C=![]() A+
A+![]() C=AC,推出当点P与
C=AC,推出当点P与![]() 重合时,P
重合时,P![]() +PC的值最小,最小值=AC的长.
+PC的值最小,最小值=AC的长.
(1)如图1,连接AC,AC交EF于O,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠OAE=∠OCF,
在△OAE和△OCF中,
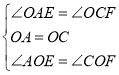 ,
,
∴△OAE≌△OCF,
∴AE=CF,
∵AE∥CF,
∴四边形AFCE是平行四边形,
由翻折得AF=CF,
∴四边形AFCE是菱形;
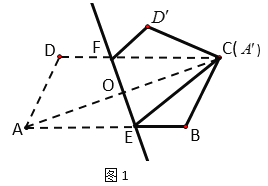
(2)①如图2,作![]() H⊥AB交AB的延长线于H,
H⊥AB交AB的延长线于H,
在Rt△GBH中,GB=![]() 2,∠GBH=60°,
2,∠GBH=60°,
∴BH=![]() ,GH=
,GH=![]() ,
,
设AE=EG=x,
在Rt△EGH中,![]() ,
,
∴![]() ,
,
解得x=![]() ,
,
∴AE=![]() ;
;
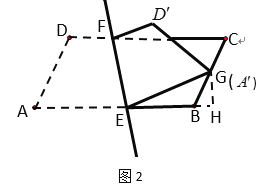
②如图3,连接AC交EF于![]() ,连接
,连接![]()
![]() ,作CH⊥AB交AB的延长线于H,
,作CH⊥AB交AB的延长线于H,
∵A、![]() 关于直线EF对称,
关于直线EF对称,
∴![]()
![]() =
=![]() A,
A,
∴![]()
![]() +
+![]() C=
C=![]() A+
A+![]() C=AC,
C=AC,
当点P与![]() 重合时,P
重合时,P![]() +PC的值最小,最小值=AC的长,
+PC的值最小,最小值=AC的长,
在Rt△BCH中,BC=4,∠CBH=60°,
∴BH=2,CH=![]() ,
,
∴AH=10,
在Rt△ACH中,AC=![]() ,
,
∴P![]() +PC的最小值为img src="http://thumb.zyjl.cn/questionBank/Upload/2020/07/22/03/1523d778/SYS202007220311032411941781_DA/SYS202007220311032411941781_DA.002.png" width="33" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,
+PC的最小值为img src="http://thumb.zyjl.cn/questionBank/Upload/2020/07/22/03/1523d778/SYS202007220311032411941781_DA/SYS202007220311032411941781_DA.002.png" width="33" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形。
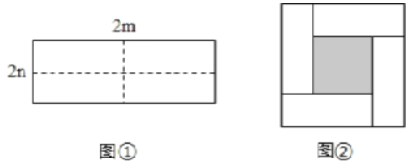
(1)用两种不同的方法表示图②中小正方形(阴影部分)的面积:
方法一:![]() ;
;
方法二:![]() .
.
(2)(m+n)![]() ,(mn)
,(mn) ![]() ,mn这三个代数式之间的等量关系为___
,mn这三个代数式之间的等量关系为___
(3)应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求xy的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3![]() 、7
、7![]() 、9
、9![]() ;乙盒子中装有4张卡片,卡片上分别写着2
;乙盒子中装有4张卡片,卡片上分别写着2![]() 、4
、4![]() 、6
、6![]() 、8
、8![]() ;盒子外有一张写着5
;盒子外有一张写着5![]() 的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果生产基地,某天安排30名工人采摘枇杷或草莓(每名工人只能做其中一项工作),并且每人每天摘0.4吨枇杷或0.3吨草莓,当天的枇杷售价每吨2000元,草莓售价每吨3000元,设安排其中x名工人采摘枇杷,两种水果当天全部售出,销售总额达y元.
(1)求y与x之间的函数关系式;
(2)若要求当天采摘枇杷的数量不少于草莓的数量,求销售总额的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校提倡练字,小冬和小红一起去文具店买钢笔和字帖,小冬在文具店买1支钢笔和3本字帖共花了38元,小红买了2支钢笔和4本字帖共花了64元.
(1)每支钢笔与每本字帖分别多少元?
(2)帅帅在六一节当天去买,正巧碰到文具店搞促销,促销方案有两种形式:
①所购商品均打九折
②买一支钢笔赠送一本字帖
帅帅要买5支钢笔和15本字帖,他有三种选择方案:
(Ⅰ)一次买5支钢笔和15本字帖,然后按九折付费;
(Ⅱ)一次买5支钢笔和10本字帖,文具店再赠送5本字帖;
(Ⅲ)分两次购买,第一次买5支钢笔,文具店会赠送5本字帖,第二次再去买10本字帖,可以按九折付费;问帅帅最少要付多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
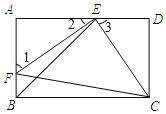
【题目】如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
(1)求证:△AEF≌△DCE;
(2)若CD=1,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
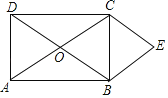
【题目】平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)当四边形ABCD是 形时,四边形OBEC是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中, ∠B=90°,DE//AB交BC于E、交AC于F,∠CDE=∠ACB=30°,BC=DE.

(1)求证:△ACD是等腰三角形;
(2)若AB=4,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顶点在网格交点的多边形叫做格点多边形,如图,在一个9 X 9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为l个单位长度.
(1)在网格中画出△ABC向上平移4个单位后得到的△AlBlCl;
(2)在网格中画出△ABC绕点A逆时针旋转900后得到的△AB2C2;
(3)在(1)中△ABC向上平移过程中,求边AC所扫过区域的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com