
| A. | 这1000名考生是总体的一个样本 | B. | 近4万名考生是总体 | ||
| C. | 1000名学生是样本容量 | D. | 每位考生的数学成绩是个体 |
分析 总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
解答 解:A、这1000名考生的数学成绩是总体的一个样本,故选项错误;
B、4万名考生的数学成绩是总体,故选项错误;
C、1000是样本容量,选项错误;
D、每位考生的数学成绩是个体,故选项正确.
故选D.
点评 本题考查了总体、个体、样本、样本容量的定义,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.


科目:初中数学 来源: 题型:选择题
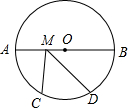 如图,在⊙O中,AB是⊙O的直径,AB=12,点C、D是$\widehat{AB}$的三等分点,M是AB上一动点,则CM+DM的最小值是( )
如图,在⊙O中,AB是⊙O的直径,AB=12,点C、D是$\widehat{AB}$的三等分点,M是AB上一动点,则CM+DM的最小值是( )| A. | 16 | B. | 12 | C. | 8 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -m2-1 | 2 | 3 | … |
| y | … | -1 | 0 | n2+1 | … |
| A. | x>2 | B. | x>3 | C. | x<2 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点O是直线AB、CD的交点,OE⊥AB,OF⊥CD,OM是∠BOF的平分线,∠AOC=32°.
如图,点O是直线AB、CD的交点,OE⊥AB,OF⊥CD,OM是∠BOF的平分线,∠AOC=32°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图(1),一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在线段OP上滑动,将窗户OM按图示方向向内旋转45°到达ON位置,如图(2),此时,点A、C的对应位置分别是点B、D,测量出∠ODB为37°,点D到点O的距离为28cm.
如图(1),一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在线段OP上滑动,将窗户OM按图示方向向内旋转45°到达ON位置,如图(2),此时,点A、C的对应位置分别是点B、D,测量出∠ODB为37°,点D到点O的距离为28cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com