

分析 (1)分三种情形画出图形,根据三角形面积公式就是即可,最后写成分段函数的格式.
(2)根据自变量取值范围,画出分段函数的图象即可.
(3)根据图象,找到最高点的自变量的值,即可解决问题.
解答 解:(1)当0≤t≤1.5时,如图1中,点M在AD上运动,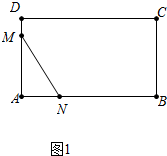
在RTAMN中,∵AM=2t,AN=t,
∴y1=$\frac{1}{2}$•AN•AM=$\frac{1}{2}$•t•2t=t2.
当1.5<t≤4.5时,如图2中,点M在DC上运动,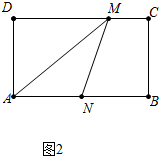
∵△AMN的高AD=3,底AN=t,
∴y2=$\frac{1}{2}$•AN•AM=$\frac{1}{2}$•t•3=1.5t.
当4.5<t≤6时,如图3中,点M在CB上运动,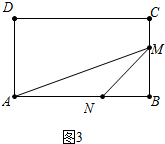
在△AMN中,∵AN=t,BM=12-2t,
∴y3=$\frac{1}{2}$AN•BM=$\frac{1}{2}$•t•(12-2t)=-t2+6t.
∴y=$\left\{\begin{array}{l}{{t}^{2}}&{(0≤t≤1.5)}\\{1.5t}&{(1.5<t≤4.5)}\\{-{t}^{2}+6t}&{(4.5<t≤6)}\end{array}\right.$.
(2)y(cm2)与t(s)之间的函数图象如下图所示,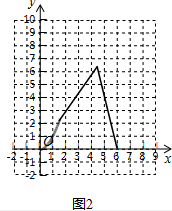
(3)由图象可知x=4,5时,y取得最大值=1.5×4.5=6.75cm2.
故答案为6.75cm2.
点评 本题考查四边形综合题、一次函数、二次函数等知识,解题的关键是正确画出图形,根据自变量的取值范围画出图象,找到最高点求最大值,属于中考常考题型.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:选择题
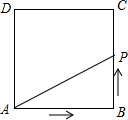 如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→B→→D→A,设P点经过的路程为x,以点A、P、B为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是( )
如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→B→→D→A,设P点经过的路程为x,以点A、P、B为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是( )| A. | 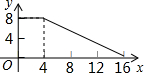 | B. | 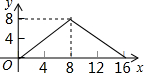 | C. | 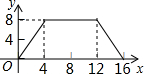 | D. | 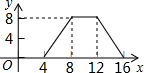 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4a-2a=2 | B. | a6÷a3=a2 | C. | ($\frac{1}{2}$)-1-22=-2 | D. | (a-b)2=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
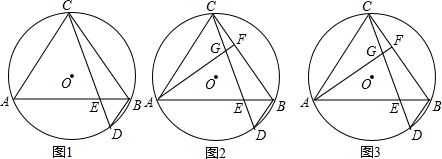
 如图所示,下列各组角的位置,判断错误的是( )
如图所示,下列各组角的位置,判断错误的是( )| A. | ∠C和∠CFG是同旁内角 | B. | ∠CGF和∠AFG是内错角 | ||
| C. | ∠BGF和∠A是同旁内角 | D. | ∠BGF和∠AFD是同位角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
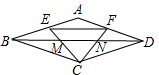 如图,在菱形ABCD中,点E、F分别是边AB、AD的中点,连接CE、CF交对角线BD于点M、N,连接EF,则BN:EF等于( )
如图,在菱形ABCD中,点E、F分别是边AB、AD的中点,连接CE、CF交对角线BD于点M、N,连接EF,则BN:EF等于( )| A. | 1:1 | B. | 1:2 | C. | 2:3 | D. | 3:2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>-1 | B. | k>-1且k≠0 | C. | k<1 | D. | k<1且k≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com