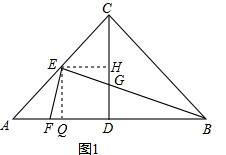
证明:作EH⊥CD,EQ⊥AB,
∵AC=BC,CD⊥AB,∠ACB=90°,
∴∠ADC=90°,∠A=∠ACD=45°,
∵EH⊥CD,EQ⊥AB,
∴∠AQE=∠EHC=90°,
又∵EA=CE,
∴△AEQ≌△ECH,
∴EQ=EH,
∵EH⊥CD,EQ⊥AB,CD⊥AB,
∴四边形EQDH是矩形,
∴∠QEH=90°,
∴∠FEQ=∠GEH=90°-∠QEB,
又∵∠EQF=∠EHG=90°,EQ=EH,
∴Rt△EFQ≌Rt△EGH,
∴EF=EG;
(2)作EH⊥CD,EQ⊥AB(如图2),
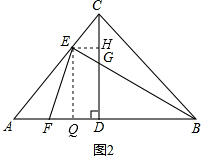
∵EH⊥CD,EQ⊥AB,CD⊥AB,
∴四边形EQDH是矩形,
∴∠QEH=90°,
∴∠FEQ=∠GEH=90°-∠QEB,
又∵∠EQF=∠EHG=90°,
∴△EFQ∽△EGH,
∴
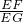
=
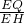
,
∵AC=BC,CD⊥AB,
∴∠ADC=90°,∠A=∠ACD=45°,
∵EH⊥CD,EQ⊥AB,
∴∠AQE=∠EHC=90°,
∴△AQE和△EHC是等腰直角三角形,
∴△AQE∽△EHC,
∴
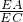
=
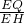
=

,
∴
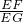
=2,
∴EF=2EG;
(3)EF=kEG.
分析:(1)作EH⊥CD,EQ⊥AB,利用AAS先证△AEQ≌△ECH,易得EQ=EH,把EQ=EH作为一个条件,再利用ASA易证Rt△EFQ≌Rt△EGH,从而有EF=EG;
(2)作EH⊥CD,EQ⊥AB,先证△EFQ∽△EGH,易得
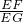
=
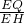
,再证△AQE∽△EHC,那么
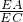
=
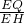
=

,等量代换易得
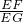
=2,于是EF=2EG;
(3)根据(1)(2)的结论易得EF=kEG.
点评:本题考查了等腰直角三角形的判定和性质、相似三角形的判定和性质、全等三角形的判定和性质、矩形的判定和性质,解题的关键是作辅助线,构造全等三角形和相似三角形,并且证明四边形EQDH是矩形.


 证明:作EH⊥CD,EQ⊥AB,
证明:作EH⊥CD,EQ⊥AB, ∵EH⊥CD,EQ⊥AB,CD⊥AB,
∵EH⊥CD,EQ⊥AB,CD⊥AB,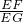 =
=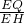 ,
,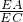 =
=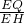 =
= ,
,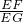 =2,
=2,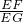 =
=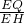 ,再证△AQE∽△EHC,那么
,再证△AQE∽△EHC,那么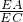 =
=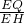 =
= ,等量代换易得
,等量代换易得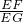 =2,于是EF=2EG;
=2,于是EF=2EG;

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为