
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点. 
(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、 ![]() ,
, ![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以它的对角线OB1为一边作正方形OB1B2C1 , 以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3C2 , 再以正方形OB2B3C2的对角线OB3为一边作正方形OB3B4C3 , …,依次进行下去,则点B6的坐标是 . 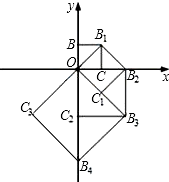
查看答案和解析>>
科目:初中数学 来源: 题型:
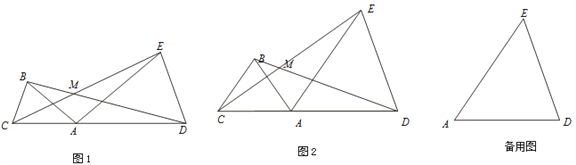
【题目】已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段 BD、CE交于点M.
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;②求∠BMC的大小(用α表示);
(2)如图2,若AB= BC=kAC,AD =ED=kAE 则线段BD与CE的数量关系为 ,∠BMC= (用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺规作图,不写作法,保留作图痕迹),连接 EC并延长交BD于点M.则∠BMC= (用α表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,定点A(1,3),B(1,1),C(3,1),规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位长度”为一次变换,如此这样,连续经过2 017次变换后,正方形ABCD的对角线交点M的坐标变为( )
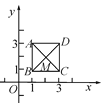
A. (-2015,2) B. (-2015,-2) C. (-2016,-2) D. (-2016,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
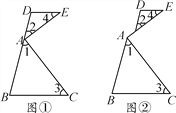
【题目】如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以O为原点的直角坐标系中,A点的坐标为(0,1),直线x=1交x轴于点B。P为线段AB上一动点,作直线PC⊥PO,交直线x=1于点C。过P点作直线MN平行于x轴,交y轴于点M,交直线x=1于点N。
(1)当点C在第一象限时,求证:△OPM≌△PCN;
(2)当点C在第一象限时,设AP长为m,四边形POBC的面积为S,请求出S与m间的函数关系式,并写出自变量m的取值范围;
(3)当点P在线段AB上移动时,点C也随之在直线x=1上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰直角三角形的点P的坐标;如果不可能,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚家装修,准备安装照明灯.他和爸爸到市场进行调查,了解到某种优质品牌的一盏40瓦白炽灯的售价为1.5元,一盏8瓦节能灯的售价为22.38元,这两种功率的灯发光效果相当.假定电价为0.45元/度,设照明时间为x(小时),使用一盏白炽灯和一盏节能灯的费用分别为y1(元)和y2(元)[耗电量(度)=功率(千瓦)×用电时间(小时),费用=电费+灯的售价].
(1)分别求出y1、y2与照明时间x之间的函数表达式;
(2)你认为选择哪种照明灯合算?
(3)若一盏白炽灯的使用寿命为2000小时,一盏节能灯的使用寿命为6000小时,如果不考虑其他因素,以6000小时计算,使用哪种照明灯省钱?省多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com