
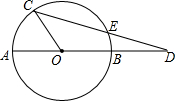
 如图所示,AB是⊙0的直径,C是⊙0上一点,∠AOC=54°,CD交⊙0于点E,且DE=0A,求∠D的度数.
如图所示,AB是⊙0的直径,C是⊙0上一点,∠AOC=54°,CD交⊙0于点E,且DE=0A,求∠D的度数. 科目:初中数学 来源: 题型:选择题
| A. | 该校七年级学生是总体 | B. | 该校七年级的每一个学生是个体 | ||
| C. | 抽出的60名学生是样本 | D. | 样本容量是60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
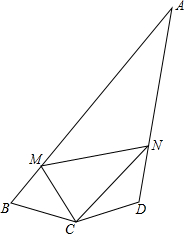 如图,四边形ABCD中,∠B+∠D=180°,∠BCD=150°,CB=CD,M,N为AB、AD上的两个动点,且∠MCN=75°.求证:MN=BM+DN.
如图,四边形ABCD中,∠B+∠D=180°,∠BCD=150°,CB=CD,M,N为AB、AD上的两个动点,且∠MCN=75°.求证:MN=BM+DN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
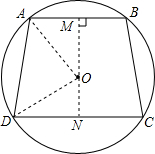 如图,⊙O中,弦AB∥CD,$\widehat{AB}+\widehat{DC}=\widehat{AD}+\widehat{BC}$,AB=10,DC=12,求梯形ABCD的面积.
如图,⊙O中,弦AB∥CD,$\widehat{AB}+\widehat{DC}=\widehat{AD}+\widehat{BC}$,AB=10,DC=12,求梯形ABCD的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>-1 | B. | m≠0 | C. | m>1且m≠0 | D. | m>-1且m≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
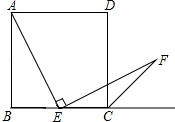 如图,点E是正方形ABCD中BC边上任意一点,以E为端点作EF=AE交∠BCD的外角平分线于F,求证:AE⊥EF.
如图,点E是正方形ABCD中BC边上任意一点,以E为端点作EF=AE交∠BCD的外角平分线于F,求证:AE⊥EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com