
【题目】如图1,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.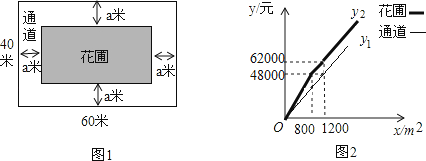
(1)用含a的式子表示花圃的面积.
(2)如果通道所占面积是整个长方形空地面积的![]() , 求出此时通道的宽.
, 求出此时通道的宽.
(3)已知某园林公司修建通道、花圃的造价y1(元)、y2(元)与修建面积x(m2)之间的函数关系如图2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价最低,最低总造价为多少元?
【答案】
(1)
【解答】解:由图可知,花圃的面积为(40﹣2a)(60﹣2a);
(2)
由已知可列式:60×40﹣(40﹣2a)(60﹣2a)=![]() ×60×40,
×60×40,
解以上式子可得:a1=5,a2=45(舍去),
答:所以通道的宽为5米;
(3)
设修建的道路和花圃的总造价为y,通道宽为a;
x花圃=(40﹣2a)(60﹣2a)=4a2﹣200a+2400;
x通道=60×40﹣(40﹣2a)(60﹣2a)=﹣4a2+200a,
由已知得y1=40(﹣4a2+200a),(2≤a≤10)
y2=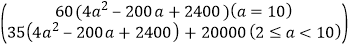
则y=y1+y2=![]()
当a=2时,y有最小值,最小值为105920;
所以当通道宽为2米时,修建的通道和花圃的总造价最低为105920元.
【解析】(1)用含a的式子先表示出花圃的长和宽后利用其矩形面积公式列出式子即可;
(2)根据通道所占面积是整个长方形空地面积的![]() , 列出方程进行计算即可;
, 列出方程进行计算即可;
(3)根据图象,设出通道和花圃的解析式,用待定系数法求解,再根据实际问题写出自变量的取值范围即可.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与EFGH均为正方形,点B、F在函数y= ![]() (x>0)的图象上,点G、C在函数y=﹣
(x>0)的图象上,点G、C在函数y=﹣ ![]() (x<0)的图象上,点A、D在x轴上,点H、E在线段BC上,则点G的纵坐标 .
(x<0)的图象上,点A、D在x轴上,点H、E在线段BC上,则点G的纵坐标 . 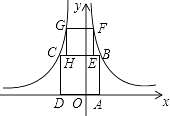
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4 ![]() ,则△CEF的周长为 .
,则△CEF的周长为 . 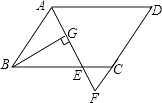
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,C、D是半圆的三等分点,延长AC,BD交于点E. 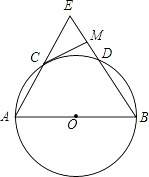
(1)求∠E的度数;
(2)点M为BE上一点,且满足EMEB=CE2 , 连接CM,求证:CM为⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com