
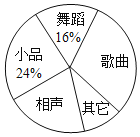
����Ŀ��ijУΪ����ף������ʮ���꣬�����ٰ�һ̨�������ᣬΪ���˽�ѧ����ϲ���Ľ�Ŀ��ʽ�������ȡ�˲���ѧ�����е��飬�涨ÿ�˴��������������赸������СƷ�������������������������ѡ����ѡ��һ�����������������Ƴ�����������������ͳ��ͼ���������ͼ����Ϣ����������⣺
��ϲ���Ľ�Ŀ | ���� |
���� | 15 |
�赸 | a |
СƷ | 12 |
���� | 10 |
���� | b |
��1���ڴ˴ε����У���Уһ���������� ����ѧ����
��2��a���� ����b���� ����
��3�������μ�ͼ�У��������������������ε�Բ�ĽǵĶ�����
��4������У����1200��ѧ�������������ϲ������������ѧ����������
���𰸡���1��50����2��8��5����3��108������4��240��.
��������
��1���ӱ����ͳ��ͼ�п��Եõ�ϲ����СƷ��������Ϊ12�ˣ�ռ����������24%�����������������
��2���赸ռ50�˵�16%�������a��ֵ���������������м�ȥ������������õ�b��ֵ��
��3���ȼ�������������ռ�İٷֱȣ���360��ȥ�˼��ɣ�
��4�������������壬������ϲ�����������İٷֱȹ�������İٷֱȣ��������������
��1��12��24%��50��
�ʴ�Ϊ50��
��2��a��50��16%��8�ˣ�
b��50��15��8��12��10��5�ˣ�
�ʴ�Ϊ��8��5��
��3��360���![]() ��108��
��108��
�����������������ε�Բ�ĽǵĶ���Ϊ108����
��4��1200��![]() ��240��
��240��
�𣺸�У1200��ѧ������ϲ������������ѧ����Լ��240�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У�����OABC�Ķ���O������ԭ���غϣ�A��C�ֱ����������ϣ���B������Ϊ��4��2����ֱ��![]() ��AB��BC�ֱ��ڵ�M��N������������
��AB��BC�ֱ��ڵ�M��N������������![]() ��ͼ����M��N��
��ͼ����M��N��

��1�����������Ľ���ʽ��
��2������P��y���ϣ�����OPM��������ı���BMON�������ȣ����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=x�뷴��������y=![]() ��k��0����ͼ���ڵ�һ�����ڽ��ڵ�A��2��m����
��k��0����ͼ���ڵ�һ�����ڽ��ڵ�A��2��m����
��1����m��k��ֵ��
��2����B��y�Ḻ�����ϣ�����AOB�����Ϊ2����AB����ֱ�ߵĺ�������ʽ��
��3������AOB��ֱ��AB����ƽ�ƣ�ƽ�ƺ�A��O��B�Ķ�Ӧ��ֱ�ΪA'��O'��B'������O'ǡ�����ڷ���������y=![]() ��ͼ����ʱ�����A'�����꣮
��ͼ����ʱ�����A'�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
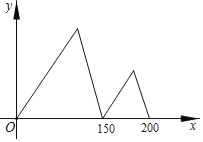
����Ŀ���ס���������ͬһֱ�ߵ�·��ͬ��㡢ͬ����ͬʱ�������ֱ��Բ�ͬ���ٶ������ܲ�1000�ף��׳�����150��ʱ����ͣ�����Ⱥ��ң��ס��һ�Ϻ����˷ֱ���ԭ�����ٶȼ��������յ㣬�ȵ��յ�������յ���Ϣ�����ܲ������������У��ס������˵ľ���y���ף����ҳ�����ʱ��x���룩֮��Ĺ�ϵ��ͼ��ʾ������յ�ʱ���Ҿ����յ㻹��_____�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������Ļ�����ʶ��ij�з��������ܼ��ţ���ɫ�������ij�����ij��ҵץס����Ͷ��20��Ԫ����Ͷ��һ��A������������������Ϊ�������������ӣ��ƻ�����Ͷ��B�͵�����B�͵�����Ͷ��������A�͵�����Ͷ��������ͬ��Ͷ���ܷ��ü���20%������B�͵����ĵ��۱ȹ���A�͵����ĵ�����50Ԫ����A�͵���ÿ�����ļ۸��Ƕ���Ԫ����A�͵���ÿ�����ļ۸�ΪxԪ���������⣬�з�����ȷ���ǣ�������
A.![]() ��
��![]()
B.![]() ��
��![]()
C.![]() ��
��![]()
D.![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
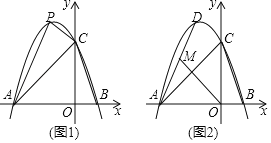
����Ŀ����ͼ��������y��ax2+bx+c����A����3��0����B��1��0����C��0��3�����㣮
��1���������ߵĺ�������ʽ��
��2����ͼ1��PΪ���������ڵڶ������ڵ�һ�㣬����PAC���Ϊ3�����P�����ꣻ
��3����ͼ2��DΪ�����ߵĶ��㣬���߶�AD���Ƿ���ڵ�M��ʹ����M��A��OΪ��������������ABC���ƣ������ڣ����M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Գ�����OBCD�Ķ���OΪ����ԭ�㽨��ƽ��ֱ������ϵ��B������Ϊ��0��a����C������Ϊ��c��b������a��b��C����![]() +|2b+12|+��c��4��2��0��
+|2b+12|+��c��4��2��0��

��1����B��C��������ꣻ
��2������P�ӵ�O��������O��B��C��·����ÿ��2����λ���ȵ��ٶ������˶������P���˶�ʱ��Ϊt�룬DC����һ��M��4����3�����ú�t��ʽ�ӱ�ʾ������OPM�������
��3����tΪ��ֵʱ��������OPM������dz�����OBCD�����![]() ��ֱ��д����ʱ��P�����꣮
��ֱ��д����ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ӽ�Ŀ�����ܰ��ֵ���������������Сѧ����ϲ����С����֪�������ϲ����λ���ֵ����������ڱ�У�����ȡ��һ����ѧ�����г�飨ÿ��ֻ��ѡһ���Լ���ϲ�������ֵ�����������������������������Ƴ���ͼ������������ͳ��ͼ������ͼ���ṩ����Ϣ����������⣺

��1�����α������ѧ���ж����ˣ�
��2��������ͳ��ͼ����������
��3����С������ѧУ��2000��ѧ���������ͼ����Ϣ������ȫУϲ����Angelababy����������
��4������3��ϲ���������ѧ����2��ϲ����Angelababy����ѧ���������ȡ���˲μ������������˶���ϲ���������ѧ���ĸ�����________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�Oֱ����AC�ǡ�O�ң���D��![]() ���е㣬��DE��AB������ΪF��DE��AC�ڵ�G��
���е㣬��DE��AB������ΪF��DE��AC�ڵ�G��
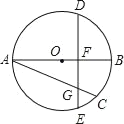
��1��������E����O������ME����AC���ӳ����ڵ�M���벹����ͼ�Σ������ʣ�ME��MG�Ƿ����������������֤����������������˵�����ɣ�
��2��������ڣ�2���ʵ������£���֪AF��3��FB��![]() ����AG��GM�ıȣ�
����AG��GM�ıȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com