
【题目】如图,以长方形OBCD的顶点O为坐标原点建立平面直角坐标系,B点坐标为(0,a),C点坐标为(c,b),且a、b、C满足![]() +|2b+12|+(c﹣4)2=0.
+|2b+12|+(c﹣4)2=0.

(1)求B、C两点的坐标;
(2)动点P从点O出发,沿O→B→C的路线以每秒2个单位长度的速度匀速运动,设点P的运动时间为t秒,DC上有一点M(4,﹣3),用含t的式子表示三角形OPM的面积;
(3)当t为何值时,三角形OPM的面积是长方形OBCD面积的![]() ?直接写出此时点P的坐标.
?直接写出此时点P的坐标.
【答案】(1)B点坐标为(0,﹣6),C点坐标为(4,﹣6)(2)S△OPM=4t或S△OPM=﹣3t+21(3)当t为2秒或![]() 秒时,△OPM的面积是长方形OBCD面积的
秒时,△OPM的面积是长方形OBCD面积的![]() .此时点P的坐标是(0,﹣4)或(
.此时点P的坐标是(0,﹣4)或(![]() ,﹣6)
,﹣6)
【解析】
(1)根据绝对值、平方和算术平方根的非负性,求得a,b,c的值,即可得到B、C两点的坐标;
(2)分两种情况:①P在OB上时,直接根据三角形面积公式可得结论;②P在BC上时,根据面积差可得结论;
(3)根据已知条件先计算三角形OPM的面积为8,根据(2)中的结论分别代入可得对应t的值,并计算此时点P的坐标.
(1)∵![]() |2b+12|+(c﹣4)2=0,∴a+6=0,2b+12=0,c﹣4=0,∴a=﹣6,b=﹣6,c=4,∴B点坐标为(0,﹣6),C点坐标为(4,﹣6).
|2b+12|+(c﹣4)2=0,∴a+6=0,2b+12=0,c﹣4=0,∴a=﹣6,b=﹣6,c=4,∴B点坐标为(0,﹣6),C点坐标为(4,﹣6).
(2)①当点P在OB上时,如图1,OP=2t,S△OPM![]() 2t×4=4t;
2t×4=4t;
②当点P在BC上时,如图2,由题意得:BP=2t﹣6,CP=BC﹣BP=4﹣(2t﹣6)=10﹣2t,DM=CM=3,S△OPM=S长方形OBCD﹣S△0BP﹣S△PCM﹣S△ODM=6×4![]() 6×(2t﹣6)
6×(2t﹣6)![]() 3×(10﹣2t)
3×(10﹣2t)![]() 4×3=﹣3t+21.
4×3=﹣3t+21.
(3)由题意得:S△OPM![]() S长方形OBCD
S长方形OBCD![]() (4×6)=8,分两种情况讨论:
(4×6)=8,分两种情况讨论:
①当4t=8时,t=2,此时P(0,﹣4);
②当﹣3t+21=8时,t![]() ,PB=2t﹣6
,PB=2t﹣6![]() ,此时P(
,此时P(![]() ,﹣6).
,﹣6).
综上所述:当t为2秒或![]() 秒时,△OPM的面积是长方形OBCD面积的
秒时,△OPM的面积是长方形OBCD面积的![]() .此时点P的坐标是(0,﹣4)或(
.此时点P的坐标是(0,﹣4)或(![]() ,﹣6).
,﹣6).


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:
【题目】赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=﹣ ![]() x+
x+ ![]() 上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 .
上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 . 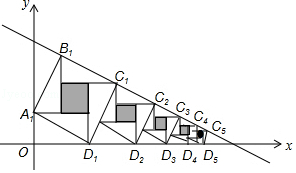
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生在校吃午餐所需时间的情况,抽查了20名同学在校吃午餐所花的时间,获得如下数据(单位:min):
10,12,15,10,16,18,19,18,20,38,
22,25,20,18,18,20,15,16,21,16.
(1)若将这些数据分为6组,请列出频数表,画出频数直方图;
(2)根据频数直方图,你认为校方安排学生吃午餐时间多长为宜?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直线1上依次摆放着四个正方形和三个等腰直角三角形(阴影图形),已知三个等腰直角三角形的面积从左到右分别为1、2、3,四个正方形的面积从左到右依次是S1、S2、S3、S4,则S1+S2+S3+S4的值为( )

A. 4 B. 5 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=120°,BC=1,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 . 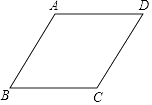
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂为了解工人在单位时间内加工同一种零件的技能水平,随机抽取了50名工人加工的零件进行检测,统计出他们各自加工的合格品数是1到8这八个整数,现提供统计图的部分信息如图.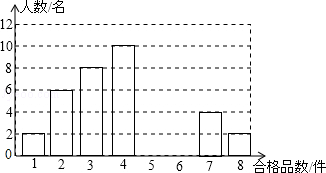
请解答下列问题:
(1)根据统计图,写出这50名工人加工出的合格品数的中位数.
(2)写出这50名工人加工出合格品数的众数的可能取值.
(3)厂方认定,工人在单位时间内加工出的合格品数不低于2件为技能合格,否则,将接受技能再培训,已知该厂有同类工人400名,请估计该厂将接受技能再培训的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点, ![]() 都是等边三角形,连接BN
都是等边三角形,连接BN
![]() 求证:
求证: ![]() ;
;
![]() 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系![]() 不需证明
不需证明![]() ;
;
![]() 如图4,当
如图4,当![]() 时,证明:
时,证明: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOC与∠BOD都是直角,∠BOC=65°
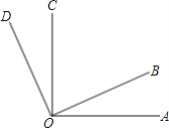
(1)求∠AOD的度数;
(2)∠AOB与∠DOC有何大小关系?
(3)若不知道∠BOC的具体度数,其他条件不变,(2)的关系仍成立吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com