【题目】如图，在菱形ABCD中，∠BAD=120°，BC=1，点P是这个菱形内部或边上的一点，若以点P、B、C为顶点的三角形是等腰三角形，则P、D（P、D两点不重合）两点间的最短距离为 ．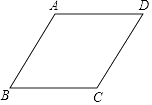 
【答案】
﹣1
【解析】解：在菱形ABCD中， ∵∠BAD=120°，BC=1，
∴△ABC，△ACD都是等边三角形，①若以边BC为底，则BC垂直平分线上（在菱形的边及其内部）的点满足题意，此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短“，即当点P与点A重合时，PD值最小，最小值为2；②若以边PC为底，∠PBC为顶角时，以点B为圆心，BC长为半径作圆，与BD相交于一点，则弧AC（除点C外）上的所有点都满足△PBC是等腰三角形，当点P在BD上时，PD最小，最小值为 ﹣1；③若以边PB为底，∠PCB为顶角，以点C为圆心，BC为半径作圆，则弧BD上的点A与点D均满足△PBC为等腰三角形，当点P与点D重合时，PD最小，显然不满足题意，故此种情况不存在；
综上所述，PD的最小值为 ﹣1．
分三种情形讨论①若以边BC为底．②若以边PC为底．③若以边PB为底．分别求出PD的最小值，即可判断．
金牌课堂练系列答案
三新快车金牌周周练系列答案科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是正方形，点E，F分别在BC，AB上，点M在BA的延长线上，且CE=BF=AM，过点M，E分别作NM⊥DM，NE⊥DE交于N，连接NF． 
（1）求证：DE⊥DM；
（2）猜想并写出四边形CENF是怎样的特殊四边形，并证明你的猜想．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，以长方形OBCD的顶点O为坐标原点建立平面直角坐标系，B点坐标为（0，a），C点坐标为（c，b），且a、b、C满足
+|2b+12|+（c﹣4）2＝0．
（1）求B、C两点的坐标；
（2）动点P从点O出发，沿O→B→C的路线以每秒2个单位长度的速度匀速运动，设点P的运动时间为t秒，DC上有一点M（4，﹣3），用含t的式子表示三角形OPM的面积；
（3）当t为何值时，三角形OPM的面积是长方形OBCD面积的
？直接写出此时点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
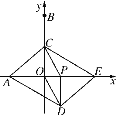
【题目】如图，在平面直角坐标系中，点A，B的坐标分别是(－3，0)，(0，6)，动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C从点B出发，沿射线BO方向以每秒2个单位的速度运动．以CP，CO为邻边构造PCOD.在线段OP延长线上一动点E，且满足PE＝AO.
(1)当点C在线段OB上运动时，求证：四边形ADEC为平行四边形；
(2)当点P运动的时间为
秒时，求此时四边形ADEC的周长是多少．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
