
【题目】如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF. 
(1)求证:DE⊥DM;
(2)猜想并写出四边形CENF是怎样的特殊四边形,并证明你的猜想.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴DC=DA,∠DCE=∠DAM=90°,
在△DCE和△MDA中, 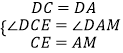 ,
,
∴△DCE≌△MDA(SAS),
∴DE=DM,∠EDC=∠MDA.
又∵∠ADE+∠EDC=∠ADC=90°,
∴∠ADE+∠MDA=90°,
∴DE⊥DM
(2)解:四边形CENF是平行四边形,理由如下:
∵四边形ABCD是正方形,
∴AB∥CD,AB=CD.
∵BF=AM,
∴MF=AF+AM=AF+BF=AB,
即MF=CD,
又∵F在AB上,点M在BA的延长线上,
∴MF∥CD,
∴四边形CFMD是平行四边形,
∴DM=CF,DM∥CF,
∵NM⊥DM,NE⊥DE,DE⊥DM,
∴四边形DENM都是矩形,
∴EN=DM,EN∥DM,
∴CF=EN,CF∥EN,
∴四边形CENF为平行四边形
【解析】(1)利用角边角可得△DCE≌△MDA,那么可得DE=DM,∠EDC=∠MDA,进而根据∠ADC=90°可得DE⊥DM;(2)先证明四边形CFMD是平行四边形,得出DM=CF,DM∥CF,再证明四边形DENM都是矩形,得出EN=DM,EN∥DM,得出CF=EN,CF∥EN,即可得出结论.
【考点精析】根据题目的已知条件,利用平行四边形的判定和正方形的性质的相关知识可以得到问题的答案,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据: ![]() ≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).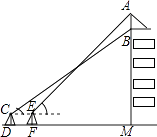
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司针对新客户优惠收费,首件物品的收费标准为:若重量不超过10千克,则免运费;当重量为![]() 千克时,运费为
千克时,运费为![]() 元;第二件物品的收费标准为:当重量为
元;第二件物品的收费标准为:当重量为![]() 千克时,运费为
千克时,运费为![]() 元。
元。
(1)若新客户所奇首件物品的重量为13千克,则运费是多少元?
(2)若新客户所寄首件物品的运费为32元,则物品的重量是多少千克?
(3)若新客户所寄首件物品与第二件物品的重量之比为2:5,共付运费为60元,则两件物品的重量各是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子元件厂准备生产4600个电子元件,甲车间独立生产一半后,由于要尽快投入市场,乙车间也加入了该电子元件的生产.若乙车间每天生产的电子元件的个数是甲车间每天生产的电子元件的个数的1.3倍,结果共用33天完成了任务.问:甲车间每天生产电子元件多少个?在这个问题中设甲车间每天生产电子元件x个,根据题意可列方程为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生在校吃午餐所需时间的情况,抽查了20名同学在校吃午餐所花的时间,获得如下数据(单位:min):
10,12,15,10,16,18,19,18,20,38,
22,25,20,18,18,20,15,16,21,16.
(1)若将这些数据分为6组,请列出频数表,画出频数直方图;
(2)根据频数直方图,你认为校方安排学生吃午餐时间多长为宜?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ ![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)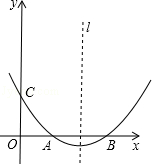
(1)求抛物线的解析式及A,B两点的坐标;
(2)若(1)中抛物线的对称轴上有点P,使△ABP的面积等于△ABC的面积的2倍,求出点P的坐标;
(3)在(1)中抛物线的对称轴l上是否存在一点Q,使AQ+CQ的值最小?若存在,求AQ+CQ的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=120°,BC=1,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 . 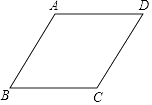
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E. 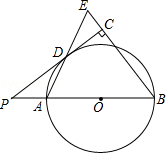
(1)求证:AB=BE;
(2)若PA=2,cosB= ![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com