
����Ŀ��ij��ݹ�˾����¿ͻ��Ż��շ�,����Ʒ���շѱ�Ϊ:������������10ǧ��,�����˷���������Ϊ![]() ǧ��ʱ,�˷�Ϊ
ǧ��ʱ,�˷�Ϊ![]() Ԫ���ڶ�����Ʒ���շѱ�Ϊ:������Ϊ
Ԫ���ڶ�����Ʒ���շѱ�Ϊ:������Ϊ![]() ǧ��ʱ,�˷�Ϊ
ǧ��ʱ,�˷�Ϊ![]() Ԫ��
Ԫ��
(1)���¿ͻ���������Ʒ������Ϊ13ǧ��,���˷��Ƕ���Ԫ?
(2)���¿ͻ���������Ʒ���˷�Ϊ32Ԫ,����Ʒ�������Ƕ���ǧ��?
(3)���¿ͻ���������Ʒ��ڶ�����Ʒ������֮��Ϊ2:5,�����˷�Ϊ60Ԫ,��������Ʒ���������Ƕ���ǧ��?
���𰸡���1��6Ԫ����2��26ǧ�ˣ���3������Ʒ������Ϊ10ǧ�ˣ��ڶ�����Ʒ������Ϊ25ǧ�ˣ�
��������
��1�������¿ͻ���������Ʒ������Ϊxǧ�ˣ�x��10��ʱ���˷�Ϊ��2x-20��Ԫ����x=13����2x-20�����㼴����⣻
��2�����ݿ�ݹ�˾����¿ͻ�����Ʒ���շѱ�����֪2x-20=32���ⷽ�̼�����⣻
��3��������Ʒ������Ϊ2aǧ�ˣ���ڶ�����Ʒ������Ϊ5aǧ�ˣ��֢�0��2a��10����2a��10��������������ۣ�
�⣺��1����13��10��
���˷�Ϊ��2��13-20=6��Ԫ����
�����¿ͻ���������Ʒ������Ϊ13ǧ�ˣ����˷���6Ԫ��
��2�������⣬��2x-20=32��
���x=26��
�����¿ͻ���������Ʒ���˷�Ϊ32Ԫ������Ʒ��������26ǧ�ˣ�
��3��������Ʒ������Ϊ2aǧ�ˣ���ڶ�����Ʒ������Ϊ5aǧ�ˣ�
�ٵ�0��2a��10����0��a��5ʱ��
2��5a+10=60�����a=5��
��ʱ2a=10��5a=25��
�ڵ�2a��10����a��5ʱ��
2��2a-20+2��5a+10=60�����a=5��
a������5��
���������������⣬��ȥ��
���ϣ�����Ʒ������Ϊ10ǧ�ˣ��ڶ�����Ʒ������Ϊ25ǧ�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O������D���Խ���BD�Ĵ��߽�BA���ӳ����ڵ�E�� 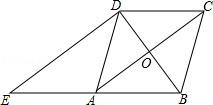
��1��֤�����ı���ACDE��ƽ���ı��Σ�
��2����AC=8��BD=6�����ADE���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽���ɽ��֦�����������ij���ŶԸ��г���������֦Ʒ��A��B��C��6���ϰ��µ����۽��е���ͳ�ƣ����Ƴ���������ͳ��ͼ��������������������ͼ�е���Ϣ������������⣺ 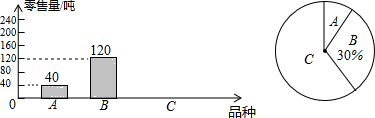
��1�����г�6���ϰ��¹�������������֦���ٶ֣�
��2����ȫͼ1��ͳ��ͼ������ͼ2��A�������ε�Բ�ĽǵĶ�����
��3��ij�̳��ƻ������°��½���A��B��C������֦��300ǧ�ˣ����ݸ��г�6���ϰ��µ��������������̳�Ӧ����CƷ����֦����ǧ�˱ȽϺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ʵء���С����ͬ��С��ֱ��������2����2��3�����һ�������Ŀڴ����ȣ���������һ��С��������a�Żؿڴ��н��ȣ�����������һ��С���ּ�������b�������͵õ�һ��������꣨a��b����
��1��������㣨a��b��ǡ���ں���y=��x��ͼ���ϵĸ��ʣ������á�����״ͼ�����б����ȷ��������������̣�����������
��2����������ڴ�������n��n��1������������2��С����ͬ���IJ������̣����õ��ĵ㣨a��b��ǡ���ں���y=��x��ͼ���ϵĸ����������ú�n�Ĵ���ʽֱ��д���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬D��F��AB���ϵ����㣬��DFΪֱ���ġ�O��BC�ཻ�ڵ�E������EF����F��FG��BC�ڵ�G�����С�OFE= ![]() ��A��
��A�� 
��1����֤��BC�ǡ�O�����ߣ�
��2����sinB= ![]() ����O�İ뾶Ϊr�����EHG��������ú�r�Ĵ���ʽ��ʾ����
����O�İ뾶Ϊr�����EHG��������ú�r�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������绷����(��6��5��)��ij�з�����һ�ݿ��������ij������鱨�棬���и���2��5����������25�����������������������±���ʾ��

(1)�Թ��Ƹ��н���Ŀ���������Ҫ���ĸ�����
(2)���ݳ������ݣ�Ԥ����н��������������Ϊ�ź�����������ԼΪ�����죿
(3)���ݵ��鱨�棬�Զ��йز�����һ����������ɫ�������Ľ��飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�������Σ���E��F�ֱ���BC��AB�ϣ���M��BA���ӳ����ϣ���CE=BF=AM������M��E�ֱ���NM��DM��NE��DE����N������NF�� 
��1����֤��DE��DM��
��2�����벢д���ı���CENF�������������ı��Σ���֤����IJ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��3a3b![]() (-2ab)+(-3a2b)2
(-2ab)+(-3a2b)2
��2��(2x+3)(2x-3)-4x(x-1)+(x-2)2
��3��![]()
![]()
![]() +(2018-
+(2018-![]() )0
)0![]()
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com