
【题目】如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE= ![]() ∠A.
∠A. 
(1)求证:BC是⊙O的切线;
(2)若sinB= ![]() ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
【答案】
(1)证明:连接OE,
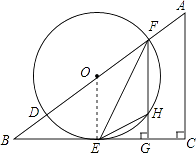
∵在△ABC中,∠C=90°,FG⊥BC,
∴∠BGF=∠C=90°,
∴FG∥AC,
∴∠OFG=∠A,
∴∠OFE= ![]() ∠OFG,
∠OFG,
∴∠OFE=∠EFG,
∵OE=OF,
∴∠OFE=∠OEF,
∴∠OEF=∠EFG,
∴OE∥FG,
∴OE⊥BC,
∴BC是⊙O的切线
(2)解:∵在Rt△OBE中,sinB= ![]() ,⊙O的半径为r,
,⊙O的半径为r,
∴OB= ![]() r,BE=
r,BE= ![]() r,
r,
∴BF=OB+OF= ![]() r,
r,
∴FG=BFsinB= ![]() r,
r,
∴BG= ![]() =
= ![]() r,
r,
∴EG=BG﹣BE= ![]() r,
r,
∴S△FGE= ![]() EGFG=
EGFG= ![]() r2,EG:FG=1:2,
r2,EG:FG=1:2,
∵BC是切线,
∴∠GEH=∠EFG,
∵∠EGH=∠FGE,
∴△EGH∽△FGE,
∴ ![]() =(
=( ![]() )2=
)2= ![]() ,
,
∴S△EHG= ![]() S△FGE=
S△FGE= ![]() r2
r2
【解析】(1)首先连接OE,由在△ABC中,∠C=90°,FG⊥BC,可得FG∥AC,又由∠OFE= ![]() ∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;(2)由在△OBE中,sinB=
∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;(2)由在△OBE中,sinB= ![]() ,⊙O的半径为r,可求得OB,BE的长,然后由在△BFG中,求得BG,FG的长,则可求得EG的长,易证得△EGH∽△FGE,然后由相似三角形面积比等于相似比的平方,求得答案.
,⊙O的半径为r,可求得OB,BE的长,然后由在△BFG中,求得BG,FG的长,则可求得EG的长,易证得△EGH∽△FGE,然后由相似三角形面积比等于相似比的平方,求得答案.


科目:初中数学 来源: 题型:
【题目】数学老师布置了一道思考题“计算:(-![]() )÷(
)÷(![]()
![]() )”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
)”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
小明的解法:原式的倒数为(![]()
![]() )÷(
)÷(![]() )=(
)=(![]()
![]() )×(-12)=-4+10=6,所以(-
)×(-12)=-4+10=6,所以(-![]() )÷(
)÷(![]()
![]() )=
)=![]() .
.
(1)请你判断小明的解答是否正确,并说明理由.
(2)请你运用小明的解法解答下面的问题.
计算:(-![]() )÷(
)÷(![]()
![]() +
+![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=﹣ ![]() x+
x+ ![]() 上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 .
上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 . 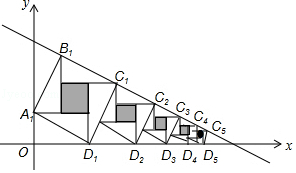
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司针对新客户优惠收费,首件物品的收费标准为:若重量不超过10千克,则免运费;当重量为![]() 千克时,运费为
千克时,运费为![]() 元;第二件物品的收费标准为:当重量为
元;第二件物品的收费标准为:当重量为![]() 千克时,运费为
千克时,运费为![]() 元。
元。
(1)若新客户所奇首件物品的重量为13千克,则运费是多少元?
(2)若新客户所寄首件物品的运费为32元,则物品的重量是多少千克?
(3)若新客户所寄首件物品与第二件物品的重量之比为2:5,共付运费为60元,则两件物品的重量各是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面几何中,我们学过两条直线平行的定义,下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.解答下面的问题:
(1)求过点P(1,2),且与已知直线y=-2x-1平行的直线l的函数解析式,并画出图象;
(2)设直线l分别与y轴,x轴交于点A、B,如果直线m:y=kx+t(t>0)与直线l平行,且交x轴于点C,求出△ABC的面积S,关于t函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子元件厂准备生产4600个电子元件,甲车间独立生产一半后,由于要尽快投入市场,乙车间也加入了该电子元件的生产.若乙车间每天生产的电子元件的个数是甲车间每天生产的电子元件的个数的1.3倍,结果共用33天完成了任务.问:甲车间每天生产电子元件多少个?在这个问题中设甲车间每天生产电子元件x个,根据题意可列方程为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生在校吃午餐所需时间的情况,抽查了20名同学在校吃午餐所花的时间,获得如下数据(单位:min):
10,12,15,10,16,18,19,18,20,38,
22,25,20,18,18,20,15,16,21,16.
(1)若将这些数据分为6组,请列出频数表,画出频数直方图;
(2)根据频数直方图,你认为校方安排学生吃午餐时间多长为宜?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com