
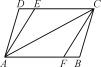
【题目】如图,要判定AB∥CD,需要哪些条件?根据是什么?
【答案】①∠D+∠DAB=180°,根据是同旁内角互补,两直线平行. ②∠CEA+∠EAB=180°,根据是同旁内角互补,两直线平行或∠DEA=∠EAB,根据是内错角相等,两直线平行.③∠DCA=∠CAB,根据是内错角相等,两直线平行. ④则需∠DCF+∠AFC=180°,根据是同旁内角互补,两直线平行或∠DCF=∠BFC,根据是内错角相等,两直线平行. ⑤∠DCB+∠B=180°,根据是同旁内角互补,两直线平行.
【解析】
根据内错角相等,两直线平行找条件判定AB∥CD;根据同旁内角互补,两直线平行找条件判定AB∥CD.
①若考虑截线AD,则需∠D+∠DAB=180°,根据是同旁内角互补,两直线平行.
②若考虑截线AE,则需∠CEA+∠EAB=180°,根据是同旁内角互补,两直线平行或∠DEA=∠EAB,根据是内错角相等,两直线平行.
③若考虑截线AC,则需∠DCA=∠CAB,根据是内错角相等,两直线平行.
④若考虑截线FC,则需∠DCF+∠AFC=180°,根据是同旁内角互补,两直线平行或∠DCF=∠BFC,根据是内错角相等,两直线平行.
⑤若考虑截线BC,则需∠DCB+∠B=180°,根据是同旁内角互补,两直线平行.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
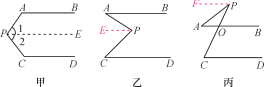
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据: ![]() ≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).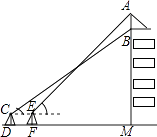
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了组织一个50人的旅游团开展“乡间民俗”游,旅游团住村民家,住宿客房有三人间、二人间、单人间三种,收费标准是三人间每人每晚20元,二人间每人每晚30元,单人间每人每晚50元,旅游团共住20间客房,旅游团如何安排住宿才能够使得住宿费最低,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=﹣ ![]() x+
x+ ![]() 上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 .
上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 . 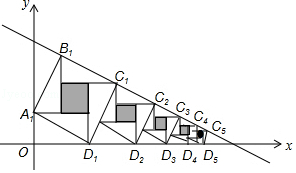
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司针对新客户优惠收费,首件物品的收费标准为:若重量不超过10千克,则免运费;当重量为![]() 千克时,运费为
千克时,运费为![]() 元;第二件物品的收费标准为:当重量为
元;第二件物品的收费标准为:当重量为![]() 千克时,运费为
千克时,运费为![]() 元。
元。
(1)若新客户所奇首件物品的重量为13千克,则运费是多少元?
(2)若新客户所寄首件物品的运费为32元,则物品的重量是多少千克?
(3)若新客户所寄首件物品与第二件物品的重量之比为2:5,共付运费为60元,则两件物品的重量各是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子元件厂准备生产4600个电子元件,甲车间独立生产一半后,由于要尽快投入市场,乙车间也加入了该电子元件的生产.若乙车间每天生产的电子元件的个数是甲车间每天生产的电子元件的个数的1.3倍,结果共用33天完成了任务.问:甲车间每天生产电子元件多少个?在这个问题中设甲车间每天生产电子元件x个,根据题意可列方程为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=120°,BC=1,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 . 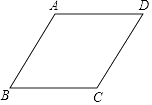
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com