练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算：

    （1）3a3b(-2ab)+(-3a2b)2

    （2）(2x+3)(2x-3)-4x(x-1)+(x-2)2

    （3） +(2018-)0

    【答案】（1）3a4b2；（2）x2-5；（3）-11.

    【解析】

    （1）先计算单项式乘以单项式和各单位的乘方，最后合并同类项即可得解；

    （2）先运用平方差公式、完全平方公式以及单项式乘以多项式把括号展开，然后再合并同类项即可；

    （3））先根据幂运算的性质计算乘方，再进一步根据有理数的加法法则计算.

    （1）原式=-6a4b2+9a4b2=3a4b2.

    （2）原式=4x2-9-(4x2-4x)+(x2-4x+4)

    =4x2-9-4x2+4x+x2-4x+4

    =x2-5.

    （3）原式=2-5+1-9=-11

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某快递公司针对新客户优惠收费,首件物品的收费标准为:若重量不超过10千克,则免运费；当重量为千克时,运费为元；第二件物品的收费标准为:当重量为千克时,运费为元。

    (1)若新客户所奇首件物品的重量为13千克,则运费是多少元?

    (2)若新客户所寄首件物品的运费为32元,则物品的重量是多少千克?

    (3)若新客户所寄首件物品与第二件物品的重量之比为2:5,共付运费为60元,则两件物品的重量各是多少千克?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+c（a≠0）的顶点坐标为（4，﹣ ），且与y轴交于点C（0，2），与x轴交于A，B两点（点A在点B的左边）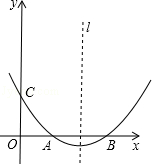

    （1）求抛物线的解析式及A，B两点的坐标；
    （2）若（1）中抛物线的对称轴上有点P，使△ABP的面积等于△ABC的面积的2倍，求出点P的坐标；
    （3）在（1）中抛物线的对称轴l上是否存在一点Q，使AQ+CQ的值最小？若存在，求AQ+CQ的最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，∠BAD=120°，BC=1，点P是这个菱形内部或边上的一点，若以点P、B、C为顶点的三角形是等腰三角形，则P、D（P、D两点不重合）两点间的最短距离为 ．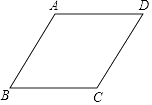

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为4的正方形ABCD中，请画出以A为一个顶点，另外两个顶点在正方形ABCD的边上，且含边长为3的所有大小不同的等腰三角形．（要求：只要画出示意图，并在所画等腰三角形长为3的边上标注数字3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)如图1，AB∥CD，则∠E＋∠G与∠B＋∠F＋∠D有何关系？

    (2)如图2，若AB∥CD，又能得到什么结论？请直接写出结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB∥CD，EF分别交AB、CD于G、F两点，射线FM平分∠EFD，将射线FM平移，使得端点F与点G重合且得到射线GN．若∠EFC=110°，则∠AGN的度数是（　　）

    A. 120° B. 125° C. 135° D. 145°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点D，过点B作BE垂直于PD，交PD的延长线于点C，连接AD并延长，交BE于点E．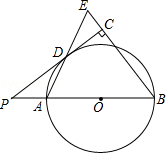
    （1）求证：AB=BE；
    （2）若PA=2，cosB= ，求⊙O半径的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某大楼的顶部树有一块广告牌CD，小李在山坡的坡脚A处测得广告牌底部D的仰角为60°．沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知山坡AB的坡度i=1： ，AB=10米，AE=15米．（i=1： 是指坡面的铅直高度BH与水平宽度AH的比）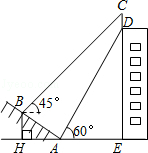

    （1）求点B距水平面AE的高度BH；
    （2）求广告牌CD的高度．
    （测角器的高度忽略不计，结果精确到0.1米．参考数据： 1.414， 1.732）

    查看答案和解析>>

    同步练习册答案