
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ ![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)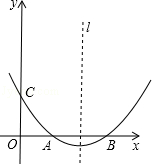
(1)求抛物线的解析式及A,B两点的坐标;
(2)若(1)中抛物线的对称轴上有点P,使△ABP的面积等于△ABC的面积的2倍,求出点P的坐标;
(3)在(1)中抛物线的对称轴l上是否存在一点Q,使AQ+CQ的值最小?若存在,求AQ+CQ的最小值;若不存在,请说明理由.
【答案】
(1)
解:抛物线的顶点坐标为(4,﹣ ![]() ),可以假设抛物线为y=a(x﹣4)2﹣
),可以假设抛物线为y=a(x﹣4)2﹣ ![]() 把点(0,2)代入得到a=
把点(0,2)代入得到a= ![]() ,
,
∴抛物线的解析式为y= ![]() (x﹣4)2﹣
(x﹣4)2﹣ ![]() .
.
令y=0得到 ![]() (x﹣4)2﹣
(x﹣4)2﹣ ![]() =0,解得x=2或6,
=0,解得x=2或6,
∴A(2,0),B(6,0)
(2)
解:设P(4,m),
由题意: ![]() 4|m|=2×
4|m|=2× ![]() ×4×2,解得m=±4,
×4×2,解得m=±4,
∴点P坐标(4,4)或(4,﹣4)
(3)
解:存在.理由如下:
∵A、B关于对称轴对称,连接CB交对称轴于Q,连接QA,此时QA+QC最短(两点之间线段最短),
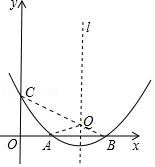
∴QA+QC的最小值=QA+QC=QB+QC=BC= ![]() =
= ![]() .
.
【解析】(1)因为抛物线的顶点坐标为(4,﹣ ![]() ),所以可以假设抛物线为y=a(x﹣4)2﹣
),所以可以假设抛物线为y=a(x﹣4)2﹣ ![]() 把点(0,2)代入得到a=
把点(0,2)代入得到a= ![]() ,令y=0,解方程即可求出A、B两点坐标.(2)设P(4,m),由题意可得
,令y=0,解方程即可求出A、B两点坐标.(2)设P(4,m),由题意可得 ![]() 4|m|=2×
4|m|=2× ![]() ×4×2,解方程即可.(3)存在.因为A、B关于对称轴对称,连接CB交对称轴于Q,连接QA,此时QA+QC最短(两点之间线段最短),
×4×2,解方程即可.(3)存在.因为A、B关于对称轴对称,连接CB交对称轴于Q,连接QA,此时QA+QC最短(两点之间线段最短),
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了解南山荔枝的销售情况,某部门对该市场的三种荔枝品种A,B,C在6月上半月的销售进行调查统计,绘制成如下两个统计图(均不完整),请你结合图中的信息,解答下列问题: 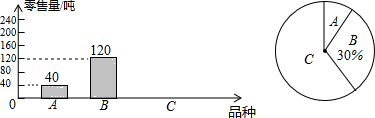
(1)该市场6月上半月共销售这三种荔枝多少吨?
(2)补全图1的统计图并计算图2中A所在扇形的圆心角的度数;
(3)某商场计划六月下半月进货A、B、C三种荔枝共300千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年世界环境日(即6月5日),某市发布了一份空气质量的抽样调查报告,其中该市2~5月随机调查的25天各空气质量级别的天数如下表所示:

(1)试估计该市今年的空气质量主要是哪个级别?
(2)根据抽样数据,预测该市今年空气质量级别为优和良的天数共约为多少天?
(3)根据调查报告,试对有关部门提一条建设“绿色城市”的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF. 
(1)求证:DE⊥DM;
(2)猜想并写出四边形CENF是怎样的特殊四边形,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)求证:BE=CF;
(2)如果AB=8,AC=6,求AE、BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AD=BC,AB=CD,AD>AB,将长方形ABCD折叠,使点C与点A重合,折痕为MN,连接CN.若△CDN的面积与△CMN的面积比为1:3,
(1)求证:DN=BM;(2)求ND:NA的值;(3)求MN2:BM2的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com