
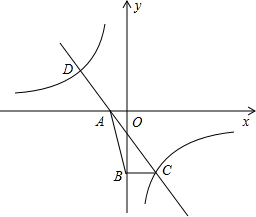
 (2013•德阳)如图,直线y=kx+k(k≠0)与双曲线y=
(2013•德阳)如图,直线y=kx+k(k≠0)与双曲线y=| n+1 |
| x |
| 17 |
| 1 |
| 2 |
| 8 |
| x |
| 17 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
|
|
|
| 8 |
| 3 |


科目:初中数学 来源: 题型:
 (2013•德阳)如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )
(2013•德阳)如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )查看答案和解析>>
科目:初中数学 来源: 题型:
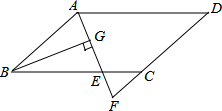 (2013•德阳)如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=4
(2013•德阳)如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=4| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
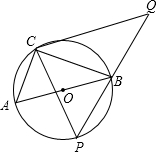 (2013•德阳)如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为
(2013•德阳)如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为| 5 |
| 2 |
| 3 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com