
【题目】如图,抛物线y=ax2+bx+2与x轴交于点A(1,0)和B(4,0).
(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;
(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:把点A(1,0)和B(4,0)代入y=ax2+bx+2得,
![]() ,
,
解得 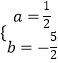 ,
,
所以,抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x+2
x+2
(2)
解:方法一:
抛物线的对称轴为直线x= ![]() ,
,
∵四边形OECF是平行四边形,
∴点C的横坐标是 ![]() ×2=5,
×2=5,
∵点C在抛物线上,
∴y= ![]() ×52﹣
×52﹣ ![]() ×5+2=2,
×5+2=2,
∴点C的坐标为(5,2)
方法二:
∵FC∥x轴,∴当FC=OE时,四边形OECF是平行四边形.
设C(t, ![]() ),
),
∴F( ![]() ,
, ![]() +2),
+2),
∴t﹣ ![]() =
= ![]() ,
,
∴t=5,C(5,2)
(3)
解:方法一:
设OC与EF的交点为D,
∵点C的坐标为(5,2),
∴点D的坐标为( ![]() ,1),
,1),
①点O是直角顶点时,易得△OED∽△PEO,
∴ ![]() ,
,
即 ![]() =
= ![]() ,
,
解得PE= ![]() ,
,
所以,点P的坐标为( ![]() ,﹣
,﹣ ![]() );
);
②点C是直角顶点时,同理求出PF= ![]() ,
,
所以,PE= ![]() +2=
+2= ![]() ,
,
所以,点P的坐标为( ![]() ,
, ![]() );
);
③点P是直角顶点时,由勾股定理得,OC= ![]() =
= ![]() ,
,
∵PD是OC边上的中线,
∴PD= ![]() OC=
OC= ![]() ,
,
若点P在OC上方,则PE=PD+DE= ![]() +1,
+1,
此时,点P的坐标为( ![]() ,
, ![]() ),
),
若点P在OC的下方,则PE=PD﹣DE= ![]() ﹣1,
﹣1,
此时,点P的坐标为( ![]() ,
, ![]() ),
),
综上所述,抛物线的对称轴上存在点P( ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ),使△OCP是直角三角形
),使△OCP是直角三角形
方法二:
∵点P在抛物线的对称轴上,设P( ![]() ,t),O(0,0),C(5,2),
,t),O(0,0),C(5,2),
∵△OCP是直角三角形,∴OC⊥OP,OC⊥PC,OP⊥PC,
①OC⊥OP,∴KOC×KOP=﹣1,∴ ![]() ,
,
∴t=﹣ ![]() ,∴P(
,∴P( ![]() ,﹣
,﹣ ![]() ),
),
②OC⊥PC,∴KOC×KPC=﹣1,∴ ![]() =﹣1,
=﹣1,
∴t= ![]() ,P(
,P( ![]() ,
, ![]() ),
),
③OP⊥PC,∴KOP×KPC=﹣1,∴ ![]() ,
,
∴4t2﹣8t﹣25=0,∴t= ![]() 或
或 ![]() ,
,
点P的坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ),
),
综上所述,抛物线的对称轴上存在点P( ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ),使△OCP是直角三角形.
),使△OCP是直角三角形.

【解析】方法一:(1)把点A、B的坐标代入函数解析式,解方程组求出a、b的值,即可得解;(2)根据抛物线解析式求出对称轴,再根据平行四边形的对角线互相平分求出点C的横坐标,然后代入函数解析式计算求出纵坐标,即可得解;(3)设AC、EF的交点为D,根据点C的坐标写出点D的坐标,然后分①点O是直角顶点时,求出△OED和△PEO相似,根据相似三角形对应边成比例求出PE,然后写出点P的坐标即可;②点C是直角顶点时,同理求出PF,再求出PE,然后写出点P的坐标即可;③点P是直角顶点时,利用勾股定理列式求出OC,然后根据直角三角形斜边上的中线等于斜边的一半可得PD= ![]() OC,再分点P在OC的上方与下方两种情况写出点P的坐标即可.
OC,再分点P在OC的上方与下方两种情况写出点P的坐标即可.
方法二:(1)略.(2)因为四边形OECF是平行四边形,且FC∥x轴,列出F,C的参数坐标,利用FC=OE,可求出C点坐标.(3)列出点P的参数坐标,分别列出O,C两点坐标,由于△OCP是直角三角形,所以分别讨论三种垂直的位置关系,利用斜率垂直公式,可求出三种情况下点P的坐标.
【考点精析】关于本题考查的二次函数的性质,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,直线![]() 分别交x、y轴于点A、C,点B在x轴负半轴上,过点A作
分别交x、y轴于点A、C,点B在x轴负半轴上,过点A作![]() 于点K,若
于点K,若![]() ,
,![]() .
.
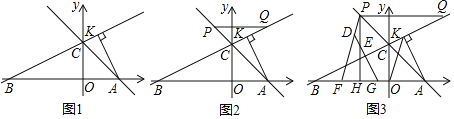
![]() 如图1,求点B坐标;
如图1,求点B坐标;
![]() 如图2,点P为AC延长线上一点,过点P作
如图2,点P为AC延长线上一点,过点P作![]() 交直线BC于点Q,设点P的横坐标为t,PQ长为d,求d与t的函数关系式
交直线BC于点Q,设点P的横坐标为t,PQ长为d,求d与t的函数关系式![]() 不必写出自变量t的取值范围
不必写出自变量t的取值范围![]() ;
;
![]() 在
在![]() 的条件下,连接OK,过点P作
的条件下,连接OK,过点P作![]() 轴于点H,点F为HB上一点,连接PF,点D在PF上,将点F沿x轴正方向平移
轴于点H,点F为HB上一点,连接PF,点D在PF上,将点F沿x轴正方向平移![]() 个单位到点G,连接DG,交PH于点E,若
个单位到点G,连接DG,交PH于点E,若![]() ,
,![]() ,
,![]() ,求点P坐标.
,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为( )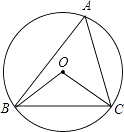
A.3 ![]()
B.4 ![]()
C.5 ![]()
D.6 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实现营养套餐的合理搭配,某电商推出两款适合不同人群的甲、乙两种袋装的混合粗粮.甲种袋装粗粮每袋含有3千克A粗粮,1千克B粗粮,1千克C粗粮;乙种袋装粗粮每袋含有1千克A粗粮,2千克B粗粮,2千克C粗粮.甲、乙两种袋装粗粮每袋成本分别等于袋中的A、B、C三种粗粮成本之和.已知每袋甲种粗粮的成本是每千克A种粗粮成本的7.5倍,每袋乙种粗粮售价比每袋甲种粗粮售价高20%,乙种袋装粗粮的销售利润率是20%.当销售这两款袋装粗粮的销售利润率为24%时,该电商销售甲、乙两种袋装粗粮的袋数之比是_____(商品的销售利润率=![]() ×100%)
×100%)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展课外体育活动,决定开设A:篮球、B:乒乓球、C:武术、D:跑步四种活动项目![]() 为了解学生最喜欢哪一种活动项目
为了解学生最喜欢哪一种活动项目![]() 每人只选取一种
每人只选取一种![]() 随机抽取了m名学生进行调查,并将调查结果绘成如下统计图,请你结合图中信息解答下列问题:
随机抽取了m名学生进行调查,并将调查结果绘成如下统计图,请你结合图中信息解答下列问题:

![]() ______;
______;
![]() 在扇形统计图中“乒乓球”所对应扇形的圆心角的度数为______;
在扇形统计图中“乒乓球”所对应扇形的圆心角的度数为______;
![]() 请把图的条形统计图补充完整;
请把图的条形统计图补充完整;
![]() 若该校有学生1200人,请你估计该校最喜欢武术的学生人数约是多少?
若该校有学生1200人,请你估计该校最喜欢武术的学生人数约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年在中央“房子是用来住的,不是用来炒”的精神作用下,房子价格持续下跌.玲玲家买了一套新房准备装修,若甲、乙两个装饰公司合作,需6周完成,共需装修费为5.2万元;若甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成,共需装修费为4.8万元.玲玲的爸爸妈妈商量后决定只选一个公司单独完成.
(1)如果从节约时间的角度考虑应选哪家公司?
(2)如果从节约开支的角度考虑应选哪家公司?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题12分)如图1,在平面直角坐标系中,四边形OABC各顶点的坐标分别O(0,0),A(3, ![]() ),B(9,5
),B(9,5 ![]() ),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3,
),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3, ![]() ,
, ![]() (单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.
(单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.

(1)求AB所在直线的函数表达式.
(2)如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值.
(3)在P,Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了监控一不规则多边形艺术走廊内的活动情况,现已在A,B两处各安装了一个监控探头(走廊内所用探头的观测区域为圆心角最大可取到180°的扇形),图中的阴影部分是A处监控探头观测到的区域.要使整个艺术走廊都能被监控到,还需再安装一个监控探头,则安装的位置是( )
A.E处
B.F处
C.G处
D.H处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家生产的一种新型节能灯,为了打开市场出台了相关政策:由厂家协调,厂家按成本价提供产品给经营户自主销售,成本价与出厂价之间的差价由厂家承担.李明按照相关政策投资销售本产品.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始销售的第一个月将销售单价定为20元,那么厂家这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么厂家为他承担的总差价最少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com