
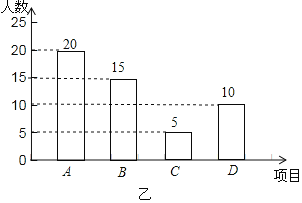
����Ŀ��ijѧУ��չ�������������������A������B��ƹ����C��������D���ܲ����ֻ��Ŀ![]() Ϊ�˽�ѧ����ϲ����һ�ֻ��Ŀ
Ϊ�˽�ѧ����ϲ����һ�ֻ��Ŀ![]() ÿ��ֻѡȡһ��
ÿ��ֻѡȡһ��![]() �����ȡ��m��ѧ�����е��飬�����������������ͳ��ͼ��������ͼ����Ϣ����������⣺
�����ȡ��m��ѧ�����е��飬�����������������ͳ��ͼ��������ͼ����Ϣ����������⣺

![]() ______��
______��
![]() ������ͳ��ͼ�С�ƹ��������Ӧ���ε�Բ�ĽǵĶ���Ϊ______��
������ͳ��ͼ�С�ƹ��������Ӧ���ε�Բ�ĽǵĶ���Ϊ______��
![]() ���ͼ������ͳ��ͼ����������
���ͼ������ͳ��ͼ����������
![]() ����У��ѧ��1200�ˣ�������Ƹ�У��ϲ��������ѧ������Լ�Ƕ��٣�
����У��ѧ��1200�ˣ�������Ƹ�У��ϲ��������ѧ������Լ�Ƕ��٣�
���𰸡���1��50��2��108�㣨3����������4��120
��������
(1)��B��Ŀ����������ռ�ٷֱȿɵ�������m��
(2)��360������B��Ŀ��Ӧ�ٷֱȿɵã�
(3)���ݸ���Ŀ����֮��Ϊ50���A��Ŀ�������ɲ�ȫͼ�Σ�
(4)����������������C��Ŀ������ռ�������ɵã�
![]() ��
��
�ʴ�Ϊ��50��
![]() ������ͳ��ͼ����ƹ����������Ӧ���ε�Բ�ĽǵĶ���Ϊ
������ͳ��ͼ����ƹ����������Ӧ���ε�Բ�ĽǵĶ���Ϊ![]() ��
��
�ʴ�Ϊ��![]() ��
��
![]() ��Ŀ����Ϊ
��Ŀ����Ϊ![]() �ˣ�
�ˣ�
��ȫͼ�����£�
![]() ���Ƹ�У��ϲ��������ѧ������Լ��
���Ƹ�У��ϲ��������ѧ������Լ��![]() �ˣ�
�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O��OAƽ����EOC��

��1������EOC=70��������BOD�Ķ�����
��2������EOC����EOD=2��3������BOD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OΪԭ�㣬��A��4��0������B��0��3�����ѡ�ABO�Ƶ�B��ʱ����ת���á�A��BO�䣬��A��O��ת��Ķ�Ӧ��ΪA�䣬O�䣬����ת��Ϊ����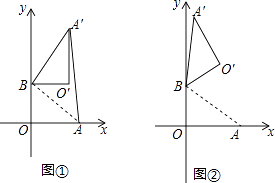
��1����ͼ�٣�����=90�㣬��AA��ij���
��2����ͼ�ڣ�����=120�㣬���O������ꣻ
��3���ڣ��������£���OA�� ��һ��P��ת��Ķ�Ӧ��ΪP�䣬��O��P+BP��ȡ����Сֵʱ�����P������ֱ꣨��д��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�������εĶ���A1����1��1����B1��1��1�����ڶ��������εĶ���A2����3��3����B2��3��3���������������εĶ���A3����6��6����B3��6��6����˳��ȡ��A1��B2��A3��B4��A5��B6�������12����Ӧȡ��B12��������Ϊ��������
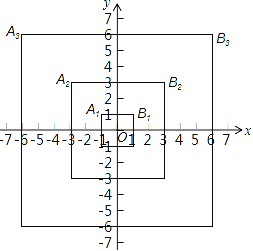
A. ��12��12�� B. ��78��78�� C. ��66��66�� D. ��55��55��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ���������蹺��һ�����Ժ͵��Ӱװ��������г������֪������1̨���Ժ�2̨���Ӱװ���3.5��Ԫ������2̨���Ժ�1̨���Ӱװ���Ҫ2.5��Ԫ��
(1)��ÿ̨���Ժ�ÿ̨���Ӱװ��������Ԫ��
(2)����ѧУ��Ҫ��ʵ�ʹ������Ժ͵��Ӱװ干30̨���ܷ���30��Ԫ������ͨ��������ѧУ�����˵��Ժ͵��Ӱװ������̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+2��x�ύ�ڵ�A��1��0����B��4��0����
��1���������ߵĽ���ʽ��
��2���������ߵĶԳ��ύx���ڵ�E����F��λ��x���Ϸ��Գ�����һ�㣬FC��x�ᣬ��Գ����Ҳ�������߽��ڵ�C�����ı���OECF��ƽ���ı��Σ����C�����ꣻ
��3���ڣ�2���������£������ߵĶԳ������Ƿ���ڵ�P��ʹ��OCP��ֱ�������Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y1=�� ![]() x��1�뷴��������y2=
x��1�뷴��������y2= ![]() ��ͼ���ڵ�A����4��m����
��ͼ���ڵ�A����4��m���� 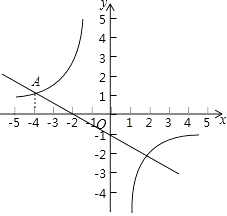
��1���۲�ͼ����y�����࣬��y1��y2ʱ����ֱ��д��x��ȡֵ��Χ��
��2����������������Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(����6��)��ͼ����ƽ��ֱ������ϵ�У���ABC�����������ֱ�ΪA(2��2)��B(4,1����C(4,4)��
��1������ ![]() ABC����ԭ��O�����ĶԳƵ�
ABC����ԭ��O�����ĶԳƵ� ![]() A1B1C1.
A1B1C1.
��2��������A����x��ĶԳƵ�A'.���ѵ�A'����ƽ��a����λ���Ⱥ����� ![]() A1B1C1���ڲ�������������ͱ߽磩����a��ȡֵ��Χ.
A1B1C1���ڲ�������������ͱ߽磩����a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y=kx+b��x���ڵ�A����y���ڵ�B��ֱ��y=2x��4��x���ڵ�D����ֱ��AB�ཻ�ڵ�C��3��2����
��1������ͼ��д������x�IJ���ʽ2x��4��x+b�Ľ⼯��
��2������A������Ϊ��5��0������ֱ��AB�Ľ���ʽ��
��3���ڣ�2���������£����ı���BODC�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com