
 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交干A、B两点,与x轴、y轴分别交于C、D两点,与x轴、y轴分别交于C,D两点,若CD=2$\sqrt{5}$,tan∠ACO=$\frac{1}{2}$,点A的坐标为(m,3).
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交干A、B两点,与x轴、y轴分别交于C、D两点,与x轴、y轴分别交于C,D两点,若CD=2$\sqrt{5}$,tan∠ACO=$\frac{1}{2}$,点A的坐标为(m,3).分析 (1)根据Rt△COD中,tan∠ACO=$\frac{1}{2}$,CD=2$\sqrt{5}$,即可得到D(0,2),C(4,0),运用待定系数法即可求得反比例函数与一次函数的解析式;
(2)先解方程组求得B(6,-1),进而得到S△AOP=2S△BOC=2×$\frac{1}{2}$×4×1=4,设P(x,-$\frac{1}{2}$x+2),再分两种情况:①当点P在CD上时,S△AOP=S△AOD+S△DOP,②当点P'在CA延长线上时,S△AOP'=S△DOP-S△AOD,分别求得点P的坐标为(2,1)或(-6,5).
解答  解:(1)∵Rt△COD中,tan∠ACO=$\frac{1}{2}$,
解:(1)∵Rt△COD中,tan∠ACO=$\frac{1}{2}$,
∴CO=2OD,
又∵CD=2$\sqrt{5}$,
∴OD2+4OD2=(2$\sqrt{5}$)2,
解得OD=2,CO=4,
∴D(0,2),C(4,0),
∵直线y=ax+b(a≠0)与x轴、y轴分别交于C、D两点,
∴$\left\{\begin{array}{l}{2=b}\\{0=4a+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴一次函数的解析式为y=-$\frac{1}{2}$x+2,
把点A的坐标(m,3)代入,可得
3=-$\frac{1}{2}$m+2,解得m=-2,
∴A(-2,3),
∵反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点A,
∴k=-2×3=-6,
∴反比例函数解析式为y=-$\frac{6}{x}$;
(2)解方程组$\left\{\begin{array}{l}{y=-\frac{1}{2}x+2}\\{y=-\frac{6}{x}}\end{array}\right.$,可得$\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=6}\\{y=-1}\end{array}\right.$,
∴B(6,-1),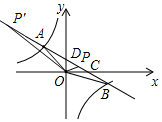
∴S△AOP=2S△BOC=2×$\frac{1}{2}$×4×1=4,
设P(x,-$\frac{1}{2}$x+2),
分两种情况:
①当点P在CD上时,S△AOP=S△AOD+S△DOP,
∴4=$\frac{1}{2}$×2×2+$\frac{1}{2}$×2×|x|,解得x=2,
∴P(2,1);
②当点P'在CA延长线上时,S△AOP'=S△DOP'-S△AOD
∴4=$\frac{1}{2}$×2×|x|-$\frac{1}{2}$×2×2,解得x=-6,
∴P'(-6,5).
综上所述,点P的坐标为(2,1)或(-6,5).
点评 本题主要考查了反比例函数与一次函数的交点问题以及解直角三角形的应用,解决问题的关键是掌握待定系数法求函数解析式的方法,解题时注意分类思想的运用.求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
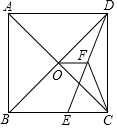 如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为( )
如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为( )| A. | 3 | B. | 4 | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠ACB=90°,CD⊥AB,垂足为点D,则下面的结论中,正确的有( )
如图,∠ACB=90°,CD⊥AB,垂足为点D,则下面的结论中,正确的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 全等三角形的对应边相等 | |
| B. | 两角一边对应相等的两个三角形全等 | |
| C. | 三边对应相等的两个三角形全等 | |
| D. | 两边一角分别相等的三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
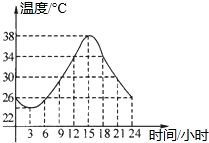 如图是某市一天的温度随时间变化的大致图象,则下列说法中错误的是( )
如图是某市一天的温度随时间变化的大致图象,则下列说法中错误的是( )| A. | 这天15时的温度最高 | |
| B. | 这天3时的温度最低 | |
| C. | 这天21时的温度是30℃ | |
| D. | 这天最高温度与最低温度的差是13℃ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com