练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．（1）计算：（$\frac{1}{2}$）-2-2sin60°+$\sqrt{12}$       
    （2）解方程：x（x+5）=x+5．

    分析 （1）利用负整数指数幂、特殊角的锐角三角函数、平方根的知识分别计算后代入求值即可；
    （2）移项后提取公因式x+5即可求解．

    解答 解：（1）原式=4-2×$\frac{\sqrt{3}}{2}$+2$\sqrt{3}$=4+$\sqrt{3}$；
    （2）移项得：x（x+5）-（x+5）=0，
    提取公因式x+5得：（x+5）（x-1）=0，
    即：x+5=0，x-1=0，
    解得：x=-5或x=1．

    点评 本题考查了因式分解法解一元二次方程、实数的运算、负整数指数幂及特殊角的三角函数值的知识，解题的关键是能够利用有关知识正确的计算，难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    1．函数y=$\frac{1}{2-x}$的定义域是x≠2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．（1）$\sqrt{12}$-$\sqrt{\frac{1}{2}}$-2$\sqrt{\frac{1}{3}}$
    （2）$（\sqrt{3}-\sqrt{2}）（\sqrt{2}-\sqrt{3}）+6\sqrt{\frac{2}{3}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

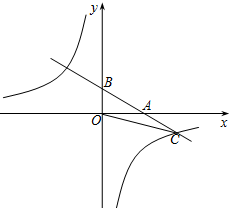    15．如图，直线y=ax+1（a≠0）与x轴交于点A，与y轴交于点B，与双曲线y=$\frac{k}{x}$在第四象限的交点为C．若点B与点C关于点A对称，且△BOC的面积为2．
    （1）求a、k的值；
    （2）问：在x轴上是否存在这样的点P，使得△PBC为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．在平面直角坐标系中，已知抛物线y=x2+bx+c与x轴交于点A（-1，0）和点B，与y轴交于点C（0，-2）．
    （1）求该抛物线的表达式，并写出其对称轴；
    （2）点D为该抛物线的顶点，设点E（m，0）（m＞2），如果△BDE和△CDE的面积相等，求E点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．解方程：
    （1）x2-3x-1=0．         
    （2）x2+4x-2=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知：如图，AB=AC=20，BC=32，D为BC边上一点，∠DAC=90°．求BD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

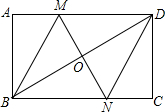    16．如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于点N，连接BM、DN．
    （1）求证：四边形BMDN是菱形；
    （2）若AB=4，AD=8，求菱形BMDN的面积和对角线MN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

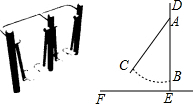    17．图中是小区常见的漫步机，当人踩在踏板上，握住扶手，像走路一样抬腿，就会带动踏板连杆绕轴旋转，从侧面看，立柱DE高1.7m，AD长0.3m，踏板静止时从侧面看与AE上点B重合，BE长0.2m，当踏板旋转到C处时，测得∠CAB=42°．求此时点C距离地面EF的高度．（结果精确到0.01m）【参考数据：sin42°=0.67，cos42°=0.74，tan42°=0.90】

    查看答案和解析>>

    同步练习册答案