
| A. | 74 | B. | 84 | C. | 75 | D. | 85 |
分析 先根据x、y为不同的正整数,且满足$\frac{1}{x}$+$\frac{1}{y}$=$\frac{2}{13}$,求出x=7,y=91,则xy+yx=791+917,再分别确定791与917的末两位数字,然后相加即可.
解答 解:将方程$\frac{1}{x}$+$\frac{1}{y}$=$\frac{2}{13}$两边同乘13xy,得13(x+y)=2xy,
∵x、y为不同的正整数,不妨设y=13t(t为正整数),则x+13t=2xt,
∴t=$\frac{x}{2x-13}$=$\frac{1}{2-\frac{13}{x}}$,
∵t为正整数,
∴1>2-$\frac{13}{x}$>0,
解得6.5<x<13,
∵x为正整数,
∴x=7,8,9,10,11,12,
当x=7时,t=$\frac{7}{2×7-13}$=7,y=13×7=91,
当x=8,9,10,11,12时,t的值均为分数,不合题意,舍去,
∴x=7,y=91,
∴xy+yx=791+917.
∵71=7,72=49,73=343,74=2401,
75=16807,76=117649,77=823543,78=5764801,
…
∴7n(n为正整数)的末两位数字以四个数字为一个周期依次循环:07,49,43,01,
∵91÷4=22…3,
∴791的末两位数字是43,
∵917的末两位数字是31,
∴791+917的末两位数字是43+31=74.
故选A.
点评 本题考查了尾数特征,数字的变化规律,代数式的恒等变形能力,不等式组的解法,能够根据条件求出x、y的值是解题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $x=\frac{5}{2}$ | B. | 3 | C. | ${x_1}=3,{x_2}=\frac{5}{2}$ | D. | ${x_1}=-\frac{5}{2},{x_2}=-3$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ±$\sqrt{\frac{16}{25}}$=±$\frac{4}{5}$ | B. | $\sqrt{\frac{16}{25}}$=±$\frac{4}{5}$ | C. | $\sqrt{\frac{16}{25}}$=$\frac{4}{5}$ | D. | ±$\sqrt{\frac{16}{25}}$=$\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
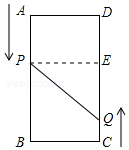 如图,A、B、C、D为矩形的四个顶点,AB=8cm,BC=3cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.
如图,A、B、C、D为矩形的四个顶点,AB=8cm,BC=3cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 近似数4.31万精确到0.01 | B. | 1.45×104精确到百位 | ||
| C. | 近似数4.60精确到十分位 | D. | 近似数5000万精确到个位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com