
ij��������һ��ÿ������Ϊ40Ԫ��С�ҵ�,���г�����Ԥ��,�ۼ۶�Ϊ50Ԫʱ���۳�400��������ÿ����1Ԫ,������������10��.
��1����ÿ���������� Ԫ,��ʱ���������Ƕ��٣����ú�
Ԫ,��ʱ���������Ƕ��٣����ú� �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��2�����������������6000Ԫ,����ʹ����������,��ÿ��Ӧ����Ϊ����Ԫ��
��3��������Ҫ����������,��ÿ��Ӧ���۶���Ԫ?��õ���������Ƕ��٣�
��1��50+x��40=x+10��Ԫ����
��2��Ҫʹ����������,��ÿ������Ϊ70Ԫ,Ӧ����200����
��3��ÿ������Ϊ65Ԫʱ���������,�ɻ�õ����������6250Ԫ��
���������������1����������=���ۼ۩������й�ϵʽ��
��2��������=ÿ���������������,������Ϊ400��10x,�з������,��������ȡ�
��3�����ú�������������ֵ��
���������������ã�
��1��50+x��40=x+10��Ԫ����
��2����ÿ����������xԪ��
�г�����Ϊ����x+10����400��10x��=6000��
��ã�x1="10" , x2=20��
Ҫʹ����������,��ÿ������Ϊ70Ԫ,Ӧ����200����
��3����ÿ����������xԪ,�������ΪyԪ��
y=��x+10����400��10x��=��10x2+300x+4000=��10��x��15��2+6250
��x=15ʱ,y�����ֵΪ6250��
����ÿ������Ϊ65Ԫʱ���������,�ɻ�õ����������6250Ԫ��
���㣺���κ�����Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵxOy�У�AB��x���ϣ���ABΪֱ���İ��O����y�������ύ�ڵ�C������BC��AC��CD�ǰ��O�������ߣ�AD��CD�ڵ�D��
��1����֤����CAD =��CAB��
��2����֪������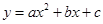 ��A��B��C���㣬AB=10��tan��CAD=
��A��B��C���㣬AB=10��tan��CAD= ��
��
�� �������ߵĽ���ʽ��
�� �ж������ߵĶ���E�Ƿ���ֱ��CD�ϣ���˵�����ɣ�
�� �����������Ƿ����һ��P��ʹ�ı���PBCA��ֱ�����Σ������ڣ�ֱ��д����P������(��д������)���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У������߾���A(-1��0),B(4��0),C(0��-4),��M�ǡ�ABC�����Բ��MΪԲ�ġ�
���������ߵĽ���ʽ��
������Ӱ���ֵ������
��������������һ��P,��PQ��x�ύBC��Q,��PQ=K,��CPQ�����ΪS,��S����K�ĺ�����ϵʽ�������S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij��װ��Ӫ��ÿ��Ĺ̶�����Ϊ300Ԫ��������һ�ֳɱ�Ϊÿ��80Ԫ�ķ�װ.�涨�����ڼ����۵��۲����ڳɱ����ۣ��һ������ø���35%.���������֣�ÿ�����۵�����Գɱ����x��Ԫ����xΪ���������վ�������y������֮��Ĺ�ϵ����һ�κ���y��kx��b���ҵ�x��10ʱ��y��100��x��20ʱ��y��80��
��1����һ�κ���y��kx��b�Ĺ�ϵʽ��
��2����÷�װ��Ӫ���վ����ë����ΪWԪ��ë�����������룭�ɱ����̶����ã�����W����x�ĺ�����ϵʽ���������۵��۶�Ϊ����Ԫʱ���վ�ë�����������վ�ë�����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ���ڡ�ABC�У�AB��AC��4cm����BAC��90�㣮����P��Qͬʱ��A��B����������ֱ���AB��BC���������ƶ������ǵ��ٶȶ���1cm/s������P�����Bʱ��P��Q����ֹͣ�˶������P���˶�ʱ��Ϊts���ı���APQC�����Ϊycm2��
��1����tΪ��ֵʱ����PBQ��ֱ��������?
��2������y��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
�ڵ�tΪ��ֵʱ��yȡ����Сֵ����СֵΪ���٣�
��3����PQ�ij�Ϊxcm������y��x�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪�����ߵĽ���ʽΪ
��1����֤������mΪ��ֵ������������x������������㣬��������A��B֮��ľ���Ϊ��ֵ��
��2�����PΪ����������һ�㣬����PAB�����Ϊ8������������ĵ�P�����ꣻ
��3������2���С�PAB�����ΪS��S>0�����Ը������Sֵ�ı仯�����ȷ�����������ĵ�P�ĸ�������С��ֱ��д�����ۣ���Ҫ��д�����㡢֤�����̣�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��������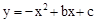 ��x�ύ��A��1��0����B��-4��0�����㣬��y����C��.
��x�ύ��A��1��0����B��-4��0�����㣬��y����C��.
(1)��������ߵĽ���ʽ.
(2)�ڸ�������λ�ڵڶ����IJ������Ƿ���ڵ�D��ʹ�á�DBC�����S��������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
(3)�������ߵĶ���Ϊ��F,�����߶�CF,����ֱ��BC,�����ܷ���ֱ��BC���ҵ�һ����M,�����������ҵ�һ����N,ʹ��C��F��M��N�ĵ���ɵ��ı���Ϊƽ���ı���,�����ڣ���д����M�͵�N�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪���κ���y=a(x-m)2-2a(x-m)��a,mΪ��������a��0��.
��1����֤������a��mΪ��ֵ���ú�����ͼ����x���������������㣻
��2����ú�����ͼ��Ķ���ΪC����x�ύ��A��B���㣬����ABC�ǵ���ֱ��������ʱ����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij������50�����乩�ο�ס�ޣ���ÿ������ķ���Ϊÿ��180Ԫʱ�������ȫ��ס������ÿ������ÿ��ķ���ÿ����10Ԫʱ���ͻ���һ��������У���������ο;�ס��ÿ������ÿ��֧��20Ԫ�ĸ��ַ��ã����ݹ涨��ÿ������ÿ��ķ��۲��ø���340Ԫ����ÿ������ķ���ÿ������xԪ��xΪ10������������
(1)��һ�충ס�ķ�����Ϊy��ֱ��д��y��x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
(2)�����һ�������ΪwԪ����w��x�ĺ�����ϵʽ��
(3)һ�충ס���ٸ�����ʱ�����ݵ����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com