
【题目】如图,∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=8,则DF等于( ) 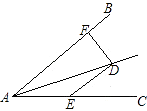
A.5
B.4
C.3
D.2
【答案】B
【解析】解:如图,∵∠DAE=∠ADE=15°,
∴∠DEG=∠DAE+∠ADE=15°+15°=30°,
DE=AE=8,
过D作DG⊥AC于G,
则DG= ![]() DE=
DE= ![]() ×8=4,
×8=4,
∵DE∥AB,
∴∠BAD=∠ADE,
∴∠BAD=∠CAD,
∵DF⊥AB,DG⊥AC,
∴DF=DG=4.
故选:B.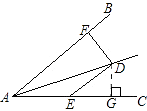
【考点精析】根据题目的已知条件,利用三角形的外角和角平分线的性质定理的相关知识可以得到问题的答案,需要掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣2,0),等边△AOC经过平移或轴对称或旋转都可以得到△OBD. 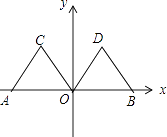
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是个单位长度;△AOC与△BOD关于直线对称,则对称轴是;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是度.
(2)连接AD,交OC于点E,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
①求证:BE=CF;
②若AF=5,BC=6,求△ABC的周长.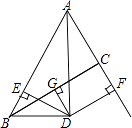
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,正确的有( )
A. 圆只有一条对称轴
B. 圆的对称轴不止一条,但只有有限条
C. 圆有无数条对称轴,每条直径都是它的对称轴
D. 圆有无数条对称轴,经过圆心的每条直线都是它的对称轴
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,l1∥l2 , C1在l1上,并且C1A⊥l2 , A为垂足,C2 , C3是l1上任意两点,点B在l2上.设△ABC1的面积为S1 , △ABC2的面积为S2 , △ABC3的面积为S3 , 小颖认为S1=S2=S3 , 请帮小颖说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有除颜色外其余均相同的5个小球,其中红球3个(记为A1,A2,A3),黑球2个(记为B1,B2).
(1)若先从袋中取出m(m>0)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:①若A为必然事件,则m的值为 ②若A为随机事件,则m的取值为
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,用树状图或列表法求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
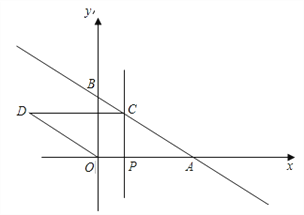
【题目】如图,已知直线y=kx+b与x轴交于A(8,0),与y轴交于B(0,6),点P是x轴正半轴上的一动点,过点P作PC⊥x轴,交直线AB于点C,以OA,AC为边构造□OACD,设点P的横坐标为m.
(1)求直线AB的函数表达式;
(2)若四边形OACD恰是菱形,请求出m的值;
(3)在(2)的条件下,y轴的上是否存在点Q,连结CQ,使得∠OQC+∠ODC=180°.若存在,直接写出所有符合条件的点Q的坐标,若不存在,则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com