
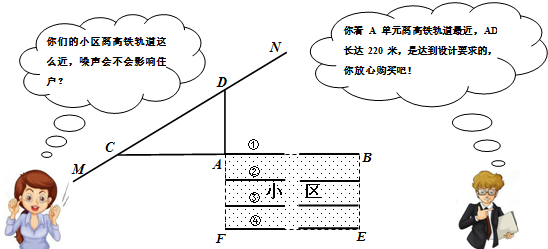
分析 (1)作过点A作AG⊥MN,垂足为G,根据三角函数可求AG的长,再与200米比较大小即可求解;
(2)在MN上找到点S、T,使得AS=AT=200米,根据勾股定理可求GT,根据三角函数可求ST,依此可求速度,进一步得到A单元用户受到影响的时间.
解答 解:(1)作过点A作AG⊥MN,垂足为G,
∵∠ACD=30°,DA⊥CA,
∴∠ADC=60°,
∵AD=220米,
∴AG=ADsin60°=110$\sqrt{3}$≈187<200,
∴A单元用户会受到影响,售楼人员的说法不可信.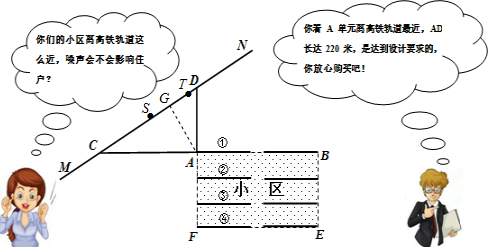
(2)在MN上找到点S、T,使得AS=AT=200米
∴GT=GS=$\sqrt{20{0}^{2}-(110\sqrt{3})^{2}}$=10$\sqrt{37}$米
∴ST=2GT=20$\sqrt{37}$≈122米
又∵速度V=$\frac{252×1000}{3600}$=70(米/秒)
∴时间t=$\frac{122+228}{70}$=5秒,即受影响的时间为5秒.
点评 此题考查了勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+4=0}\\{\frac{1}{x}-5>0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{{x}^{2}-x=0}\\{x+1<0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y+2>0}\\{x-y<0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x-5>0}\\{x<0}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
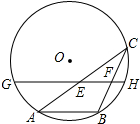 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为5,则GE+FH的最大值为7.5.
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为5,则GE+FH的最大值为7.5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com