
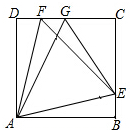
 已知,四边形ABCD为正方形,E,F分别在BC,CD上,△AEF为等边三角形,G为CD上一点,EG平分∠AGC,求证:AG=FG+EG.
已知,四边形ABCD为正方形,E,F分别在BC,CD上,△AEF为等边三角形,G为CD上一点,EG平分∠AGC,求证:AG=FG+EG. 分析 如图延长GC使得GM=GA,连接AM,EM,AM交EG于O,在GA上截取GK=FG,连接FK,先证明△EFM是等腰直角三角形,再利用“8字型”证明∠FGH=∠AEH=60°,再证明△AFK≌△EFG即可解决问题.
解答 证明:如图延长GC使得GM=GA,连接AM,EM,AM交EG于O,在GA上截取GK=FG,连接FK.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠D=∠B=∠DCB=90°,
∵△AEF是等边三角形,
∴AE=AF=EF,∠EAF=∠AEF=∠AFE=60°,
∵EG平分∠AGC,
∴GE垂直平分AM,
∴EA=EM=EF,
在RT△ADF和RT△ABE中,
$\left\{\begin{array}{l}{AD=AB}\\{AF=AE}\end{array}\right.$,
∴△ADF≌△ABE,
∴DF=BE,CF=CE,
∴∠EFC=∠FEC=∠EMF=45°,
∵∠GAM=∠GMA,∠EAM=∠EMA,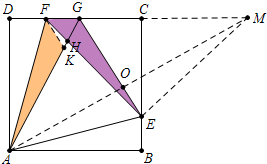
∴∠GAE=∠EMG=45°=∠GFH,
∵∠GFH+∠FHG+∠FGH=180°,∠HAE+∠AEH+∠AHE=180°,∠FHG=∠EHA,
∴∠FGH=∠AEF=60°,
∴∠AEG=∠EGC=60°,
∵GK=FG,∠FGK=60°,
∴△FGK是等边三角形,
∴FK=FG=GK,∠GFK=∠AFE=60°,
∴∠AFK=∠EFG,
在△AFK和△EFG中,
$\left\{\begin{array}{l}{AF=EF}\\{∠AFK=∠EFG}\\{FK=FG}\end{array}\right.$,
∴△AFK≌△EFG,
∴AK=EG,
∴AG=AK+GK=GE+GF.
点评 本题考查全等三角形的判定和性质、正方形的性质、等边三角形的性质,解题的关键是添加辅助线构造特殊三角形以及全等三角形,难度比较大,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com