Question

19．如图，以等边△OAB的边OB所在直线为x轴，点O为坐标原点，使点A在第一象限建立平面直角坐标系，其中△OAB边长为6个单位，点P从O点出发沿折线OAB向B点以3单位/秒的速度向B点运动，点Q从O点出发以2单位/秒的速度沿折线OBA向A点运动，两点同时出发，运动时间为t（单位：秒），当两点相遇时运动停止．
①点A坐标为（3，3$\sqrt{3}$），P、Q两点相遇时交点的坐标为（$\frac{27}{5}$，$\frac{3\sqrt{3}}{5}$）；
②当t=2时，S_△OPQ=6$\sqrt{3}$；当t=3时，S_△OPQ=$\frac{9\sqrt{3}}{2}$；
③设△OPQ的面积为S，当0＜t≤3时试求S关于t的函数关系式；
④当t=2时，试求在y轴上能否找一点M，使得以M、P、Q为顶点的三角形是直角三角形，若能找到请求出M点的坐标，若不能找到请简单说明理由．

Answer 1

分析 ①过点A作AD⊥x轴于点D，过P、Q的交点作PC⊥x轴于点C，由△AOB为等边三角形，△OAB边长为6个单位，可求出AD、OD的长度，从而得出点A的坐标；当P、Q相遇时，找出BP的长度，结合∠ABO=60°，利用三角函数值即可求出PC、CB，从而能够得出P、Q两点相遇时交点的坐标；
②当t=2时，点P运动到了A点处，OQ=4，结合三角形的面积公式即可得出此时S_△OPQ的值；当t=3时，点Q运动到了B点处，AP=3×3-OA=3，结合三角形的面积公式即可得出此时S_△OPQ的值；
③结合②的运动情况，分两段来考虑S，结合三角形的面积公式即可得出S关于t的函数关系式；
④假设存在，找出此时P、Q点的坐标，设M点的坐标为（0，m），结合两点间的距离公式以及勾股定理列出关于m的一元二次方程，解方程即可得出结论．

解答 解：①过点A作AD⊥x轴于点D，过P、Q的交点作PC⊥x轴于点C，如图1所示．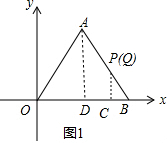

∵△AOB为等边三角形，△OAB边长为6个单位，
∴AD=OA•sin60°=3$\sqrt{3}$，AD=$\frac{1}{2}$OB=3，
∴点A的坐标为（3，3$\sqrt{3}$）；
当P、Q点相遇时点Q走过的路程为3×6÷（3+2）×2=$\frac{36}{5}$，
PB=$\frac{36}{5}$-OB=$\frac{6}{5}$，
∴BC=PB•cos60°=$\frac{3}{5}$，PC=PB•sin60°=$\frac{3\sqrt{3}}{5}$，
∴OC=OB-BC=$\frac{27}{5}$．
即P、Q相遇的坐标为（$\frac{27}{5}$，$\frac{3\sqrt{3}}{5}$）．
故答案为：（3，3$\sqrt{3}$）；（$\frac{27}{5}$，$\frac{3\sqrt{3}}{5}$）．
②依照题意画出图形，如图2所示．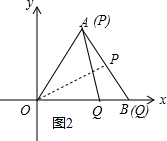

当t=2时，点P运动到了A点处，OQ=4，
S_△OPQ=$\frac{1}{2}$OA•OQ•sin∠AOQ=$\frac{1}{2}$×6×4×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$；
当t=3时，点Q运动到了B点处，AP=3×3-OA=3，
∵△OAB为等边三角形，且AB=6，
∴此时P点为线段AB的中点，
∴OP⊥AB，且∠POB=$\frac{1}{2}$∠AOB=30°，
∴OP=OB•sin∠ABO=3$\sqrt{3}$，
S_△OPQ=$\frac{1}{2}$OP•OB•sin∠POB=$\frac{1}{2}$×3$\sqrt{3}$×6×$\frac{1}{2}$=$\frac{9\sqrt{3}}{2}$．
故答案为：6$\sqrt{3}$；$\frac{9\sqrt{3}}{2}$．
③由②知当t=2时，P点运动到A点，故分两种情况考虑：
当0＜t≤2时，OP=3t，OQ=2t，
S=$\frac{1}{2}$OP•OQ•sin∠AOB=$\frac{1}{2}$×3t×2t×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}{t}^{2}$；
当2＜t≤3时，OP=3t，OQ=2t，AP=OP-OA=3t-6，BP=AB-AP=12-3t，
S=$\frac{1}{2}$OQ•BP•sin∠ABO=$\frac{1}{2}$×2t×（12-3t）×$\frac{\sqrt{3}}{2}$=-$\frac{3\sqrt{3}}{2}{t}^{2}$+6$\sqrt{3}$t．
综上可知：S关于t的函数关系式为S=$\left\{\begin{array}{l}{\frac{3\sqrt{3}}{2}{t}^{2}（0＜t≤2）}\\{-\frac{3\sqrt{3}}{2}{t}^{2}+6\sqrt{3}t（2＜t≤3）}\end{array}\right.$．
④假设存在，当t=2时，点P坐标为（3，3$\sqrt{3}$），点Q的坐标为（4，0），设点M的坐标为（0，m）．
根据两点间的距离公式可知：PQ=$\sqrt{（4-3）^{2}+（0-3\sqrt{3}）^{2}}$=2$\sqrt{7}$，PM=$\sqrt{（0-3）^{2}+（m-3\sqrt{3}）^{2}}$，QM=$\sqrt{（0-4）^{2}+{m}^{2}}$，
以M、P、Q为顶点的三角形是直角三角形分三种情况：
当PQ为斜边时，由勾股定理得PM²+QM²=PQ²，即9+$（m-3\sqrt{3}）^{2}$+16+m²=28，
方程无解；
当PM为斜边时，由勾股定理得PQ²+QM²=PM²，即28+16+m²=9+$（m-3\sqrt{3}）^{2}$，
解得：m=-$\frac{4\sqrt{3}}{9}$，此时点M的坐标为（0，-$\frac{4\sqrt{3}}{9}$）；
当QM为斜边时，由勾股定理得PQ²+PM²=QM²，即28+9+$（m-3\sqrt{3}）^{2}$=16+m²，
解得：m=$\frac{8\sqrt{3}}{3}$，此时点M的坐标为（0，$\frac{8\sqrt{3}}{3}$）．
故当t=2时，在y轴上能找到一点M，使得以M、P、Q为顶点的三角形是直角三角形，点M的坐标为（0，-$\frac{4\sqrt{3}}{9}$）或（0，$\frac{8\sqrt{3}}{3}$）．

点评 本题考查了解直角三角形、特殊角的三角函数值、三角形的面积公式、两点间的距离公式以及勾股定理，解题的关键是：①在直角三角形中借助特殊角的三角函数值求线段；②套用面积公式求面积；③分段寻找S关于t的函数关系式；④由两点间的距离公式结合勾股定理列出关于m的一元二次方程．本题属于难题，①②难度不大；③巧妙的用边乘角的正弦值来代替，使得运算量大大较少；④用到了两点间的距离公式，在作图寻找中往往会落下一两种情况，虽说两点间的距离公式为高中内容，但在日常教学中，初中的老师们往往会将此方法求距离教给学生们．