
分析 根据$\left\{\begin{array}{l}{m+2>3}\\{-\frac{m}{3}<5}\end{array}\right.$,可以求得m的取值范围,从而可以对|m+2|-|1-m|+|m|进行化简,把绝对值符号去掉,然后合并同类项即可解答本题.
解答 解:∵$\left\{\begin{array}{l}{m+2>3}\\{-\frac{m}{3}<5}\end{array}\right.$,
解得,m>1,
∴|m+2|-|1-m|+|m|
=m+2-(m-1)+m
=m+2-m+1+m
=m+3,
故答案为:m+3.
点评 本替考查解一元一次不等式组、去绝对值符号,解题的关键是根据不等式组可以确定m的取值范围,从而可以把绝对值符号去掉,需要主要的是去绝对值符号时,主要绝对值外面的符号.


 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
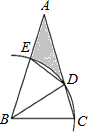 如图,△ABC中,∠A=30°,AB=AC,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E
如图,△ABC中,∠A=30°,AB=AC,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com