
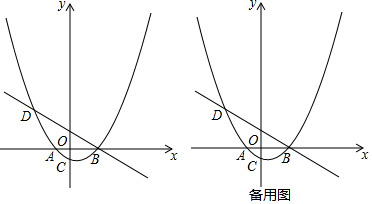
���� ��1�����������A��B���꣬Ȼ�����ֱ��BD�Ľ���ʽ����õ�D���꣬���������߽���ʽ�����a��ֵ��
��2���������ε������ʽ����������ϵʽ����ȷ�������ֵ��
��3�������⣬����M�˶���·��Ϊ����AF+DF���˶�ʱ�䣺t=AF+$\frac{1}{2}$DF����ͼ���������ߣ���AF+$\frac{1}{2}$DFת��ΪAF+FG�����ɴ��߶���̣��õ����߶�AH��ֱ��BD�Ľ��㣬��Ϊ�����F�㣮
��� �⣺��1��������y=a��x+2����x-4������y=0�����x=-2��x=4��
��A��-2��0����B��4��0����
��ֱ��y=-$\frac{\sqrt{3}}{3}$x+b������B��4��0����
��-$\frac{\sqrt{3}}{3}$��4+b=0�����b=$\frac{4\sqrt{3}}{3}$��
��ֱ��BD����ʽΪ��y=-$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$��
��x=-5ʱ��y=3$\sqrt{3}$��
��D��-5��3$\sqrt{3}$����
�ߵ�D��-5��3$\sqrt{3}$����������y=a��x+2����x-4���ϣ�
��a��-5+2����-5-4��=3$\sqrt{3}$��
��a=$\frac{\sqrt{3}}{9}$��
�������ߵĺ�������ʽΪ��y=$\frac{\sqrt{3}}{9}$x2-$\frac{2\sqrt{3}}{9}$x-$\frac{8\sqrt{3}}{9}$
��2����P��m��$\frac{\sqrt{3}}{9}$m2-$\frac{2\sqrt{3}}{9}$m-$\frac{8\sqrt{3}}{9}$��
��S��BPD=$\frac{1}{2}$��9[��-$\frac{\sqrt{3}}{3}$m+$\frac{4\sqrt{3}}{3}$��-��$\frac{\sqrt{3}}{9}$m2-$\frac{2\sqrt{3}}{9}$m-$\frac{8\sqrt{3}}{9}$��]
=-$\frac{\sqrt{3}}{2}$m2-$\frac{\sqrt{3}}{2}$m+10$\sqrt{3}$
=-$\frac{\sqrt{3}}{2}$��m+$\frac{1}{2}$��2+$\frac{81\sqrt{3}}{8}$
���BPD��������ֵΪ$\frac{81\sqrt{3}}{8}$��
��3����ͼ��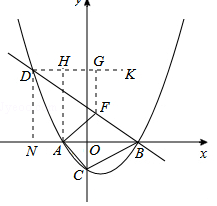
��DK��AB��AH��DK��AH��ֱ��BD�ڵ�F��
���ɣ�2���ã�DN=3$\sqrt{3}$��BN=9��
�ߡ�DBA=30�㣬
���BDH=30�㣬
��FG=DF��sin30��=$\frac{1}{2}$FD��
�൱�ҽ���AH��DKʱ��AF+FH��С��
��M�������˶�����ʱΪ��t=AF+$\frac{1}{2}$FD=AF+FH��
��lBD��y=-$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$��
��Fx=Ax=-2��F��-2��2$\sqrt{3}$��
�൱F����Ϊ��-2��2$\sqrt{3}$��ʱ����ʱ���٣�
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ�����������ε������ʽ��������ֵ��ȷ���������⣨1���Ĺؼ����ô���ϵ���������D�����꣬�⣨2���Ĺؼ����������ε������ʽ����������ϵʽ���⣨3���Ĺؼ������������ߣ���һ���ѶȱȽϴ���п������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��2�� | B�� | ��1��-2�� | C�� | ��-1��2�� | D�� | ��-1��-2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
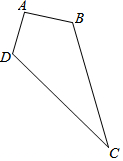 ������ĸ�ľ����β�����������������ݶ����ӣ����ܹ���һ��ƽ��ͼ�Σ�
������ĸ�ľ����β�����������������ݶ����ӣ����ܹ���һ��ƽ��ͼ�Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
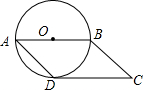 ��ͼ������ƽ���ı���һ��ABΪֱ����Բǡ�����CD�����ڵ�D�����C�Ķ����ǣ�������
��ͼ������ƽ���ı���һ��ABΪֱ����Բǡ�����CD�����ڵ�D�����C�Ķ����ǣ�������| A�� | 40�� | B�� | 45�� | C�� | 50�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
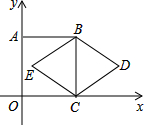 ��ͼ��������ABCO�Ķ���C��A�ֱ���x�ᡢy���ϣ�BC������BDCE�ĶԽ��ߣ�����D=60�㣬BC=2�����E�������ǣ�2-$\sqrt{3}$��1����
��ͼ��������ABCO�Ķ���C��A�ֱ���x�ᡢy���ϣ�BC������BDCE�ĶԽ��ߣ�����D=60�㣬BC=2�����E�������ǣ�2-$\sqrt{3}$��1�����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com