
科目:初中数学 来源:2014-2015学年四川省阶段S校九年级联考二数学试卷(解析版) 题型:解答题
(9分)【问题引入】
几个人拎着水桶在一个水龙头前面排队打水,水桶有大有小.他们该怎样排队才能使得总的排队时间最短?
假设只有两个人时,设大桶接满水需要T分钟,小桶接满水需要t分钟(显然T>t),若拎着大桶者在拎小桶者之前,则拎大桶者可直接接水,只需等候T分钟,拎小桶者一共等候了(T+t)分钟,两人一共等候了(2T+t)分钟;反之,若拎小桶者在拎大桶者之前,容易求出两人接满水等候(T+2t)分钟。可见,要使总的排队时间最短。拎小桶者应排在拎大桶者前面。这样,我们可以猜测,几个人拎着水桶在一个水龙头前面排队打水,要使总的排队时间最短,需将他们按水桶从小到大排队.
规律总结:
事实上,只要不按照从小到大的顺序排队,就至少有紧挨着的两个人拎大桶者排在拎小桶者之前,仍设大桶接满水需要T分钟,小桶接满水需t分钟,并设拎大桶者开始接水时已经等候了m分钟,这样拎大桶者接满水一共等候了(m+T)分钟,拎小桶者接满水一共等候了(m+T+t)分钟,两人共等候了(2m+2T+t)分钟,在其他人位置不变的前提下,让这两个人交换位置,即局部调整这两个人的位置,同样可以计算两个人接满水共等候了 __ ___分钟,共节省了 _________分钟,而其他人的等候时间未变。这说明只要存在有紧挨着的两个人是拎大桶者在拎小桶者前,都可以这样局部调整,从而使得总等候时间减少。这样经过一系列调整之后,整个队伍都是从小到大排列,就达到最优状态,总的排队时间就最短.
【方法探究】
一般地,对某些涉及多个可变对象的数学问题,先对其少数对象进行调整,其他对象暂时保持不变,从而化难为易,取得问题的局部解决.经过若干次这种局部的调整,不断缩小范围,逐步逼近目标,最终使问题得到解决,这种数学思想方法就叫做局部调整法.
【实践应用1】
如图1,在锐角△ABC中,AB=4 ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?
,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?
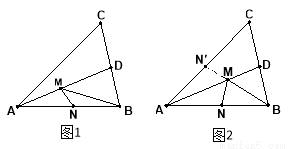
解析:(1)先假定N为定点,调整M到合适位置,使BM+MN有最小值(相对的).
容易想到,在AC上作AN′=AN(即作点N关于AD的对称点N′),连接BN′交AD于M,则M点是使BM+MN有相对最小值的点.(如图2,M点确定方法找到)
(2)再考虑点N的位置,使BM+MN最终达到最小值.
可以理解,BM+MN = BM+MN′,所以要使BM+MN′有最小值,只需使 ,此时BM+MN的最小值为 .
【实践应用2】
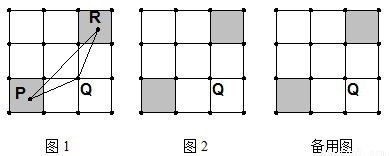
如图,把边长是3的正方形等分成9个小正方形,在有阴影的两个小正方形内(包括边界)分别任取点P、R,与已知格点Q(每个小正方形的顶点叫做格点)构成三角形,求△PQR的最大面积,并在图2中画出面积最大时的△PQR的图形.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省盘锦市中考模拟考试二数学试卷(解析版) 题型:解答题
(10分)温度通常有两种表示方法:华氏度(单位: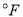 )与摄氏度(单位:
)与摄氏度(单位: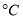 ),已知华氏度数
),已知华氏度数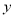 与摄氏度数
与摄氏度数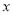 之间是一次函数关系,下表列出了部分华氏度与摄氏度之间的对应关系:
之间是一次函数关系,下表列出了部分华氏度与摄氏度之间的对应关系:

(1)选用表格中给出的数据,求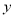 关于
关于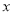 的函数解析式(不需要写出该函数的定义域);
的函数解析式(不需要写出该函数的定义域);
(2)已知某天的最低气温是-5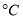 ,求与之对应的华氏度数;
,求与之对应的华氏度数;
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省盘锦市中考模拟考试二数学试卷(解析版) 题型:填空题
冬天的雪是我们的乐园,一次下雪后,小伙伴们堆了一大雪人,准备给雪人制作一个底面半径为9cm,母线长为30cm的圆锥形礼帽,则这个圆锥形礼帽的侧面积为 cm2 .(结果保留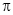 )
)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省盘锦市中考模拟考试二数学试卷(解析版) 题型:选择题
如图,直线AB∥CD,∠A=70,∠C=40,则∠E等于( )
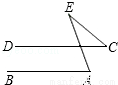
A.30° B.40° C.60° D.70°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市高新区九年级毕业暨升学模拟考试数学试卷(解析版) 题型:解答题
(本题满分8分)如图,在平面直角坐标系中,点A在第一象限,AB⊥x轴,B(2,0),tan∠AOB=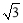 ,过点A的双曲线为
,过点A的双曲线为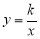 ,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的对应线段O'B'.
,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的对应线段O'B'.
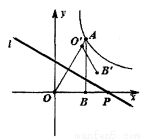
(1)当点O'与点A重合时,求直线l的解析式:
(2)当点B'落在双曲线上时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市高新区九年级毕业暨升学模拟考试数学试卷(解析版) 题型:选择题
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2015次碰到矩形的边时,点P的坐标为( )
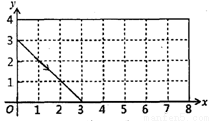
A.(3,0) B.(7,4) C.(8,1) D.((1,4)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期末试卷数学试卷(解析版) 题型:解答题
(本题满分10分)如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与AC,AB的交点分别为D,E.

(1)若AD=15,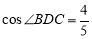 ,求AC的长和
,求AC的长和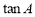 的值;
的值;
(2)若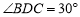 ,求
,求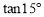 的值.(结果保留根号)
的值.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com