
当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为
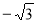 或2
或2
【解析】
试题分析:二次函数y=-(x-m)²+m²+1的顶点为(m,m²+1),
(1)当m<-2时,顶点(对称轴 x=m)在-2≤x≤1范围左侧,此时函数在-2≤x≤1范围内y随着x的增大而减小,所以当x=-2时,y最大,所以4=-(-2-m)²+m²+1,解得m=-7/4,因m<-2,所以m=-7/4舍去;
(2)当-2≤m≤1时,顶点(对称轴 x=m)在-2≤x≤1范围内,所以当x=m时,y有最大值,所以4=m²+1解得:m=±√3,因-2≤m≤1,所以m=√3舍去,所以m=-√3;
(3)当m>1时,顶点(对称轴 x=m)在-2≤x≤1范围右侧,此时函数在-2≤x≤1范围内y随着x的增大而增大,所以当x=1时,y最大,所以4=-(1-m)²+m²+1,解得m=2,
综上得当m=-√3或m=2时,二次函数y=-(x-m)²+m²+1在-2≤x≤1范围内有最大值时4.
考点:1.二次函数的性质;2.二次函数的最值.


科目:初中数学 来源:2014-2015学年浙江省嘉兴市实验初学七年级上学期期中考试数学试卷(解析版) 题型:解答题
(6分)先阅读下面例题的解题过程,再解答后面的题目。
例:已知代数式 ,求
,求 的值。
的值。
【解析】
由  得
得  即
即 
因此  , 所以
, 所以 
题目:已知代数式 ,求
,求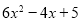 的值。
的值。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省宁波市九年级10月月考数学试卷(解析版) 题型:解答题
(本题满分14分)如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线y=x2+bx+c经过点B,且顶点在直线x=上.

(1)求抛物线对应的函数关系式;
(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标;
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省宁波市部九年级上学期第一次月考数学试卷(解析版) 题型:填空题
如图是二次函数 和一次函数
和一次函数 的图象,观察图象写出
的图象,观察图象写出 时,x的取值范围________.
时,x的取值范围________.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省宁波市部九年级上学期第一次月考数学试卷(解析版) 题型:解答题
如图1,在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),A点坐标为(-1,0)OB=OC ,
(1)求这个二次函数的表达式.
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(3)如图2,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.

图1 图2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省嘉兴市八年级上学期期中考试数学试卷(解析版) 题型:填空题
某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5 %,则至多可打 折.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省富阳市共同体九年级10月月考数学试卷(解析版) 题型:填空题
如图,抛物线 与
与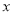 轴正半轴交于点A(3,0).以OA为边在
轴正半轴交于点A(3,0).以OA为边在 轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则
轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则 = ,点E的坐标是 .
= ,点E的坐标是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省联盟七年级上学期期中数学试卷(解析版) 题型:填空题
下列定义一种关于正整数 的“F运算”:①当
的“F运算”:①当 是奇数时,F=3
是奇数时,F=3 +5;
+5;
②当 为偶数时,结果是F=
为偶数时,结果是F= ×
× ×
× ×
× ×…(其中F是奇数),并且重复进行.
×…(其中F是奇数),并且重复进行.
例如:取 =26,如图,
=26,如图,

若 =50,则第2次“F运算”的结果是 ;第2014次“F运算”的结果是 .
=50,则第2次“F运算”的结果是 ;第2014次“F运算”的结果是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com