
如图1,在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),A点坐标为(-1,0)OB=OC ,
(1)求这个二次函数的表达式.
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(3)如图2,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.

图1 图2
(1)二次函数的表达式为:y=x2-2x-3;
(2)存在,F(2,-3);理由见解析;
(3)当x= 时,△APG的面积最大为
时,△APG的面积最大为 ;此时P点的坐标为(
;此时P点的坐标为( ,-
,- ).
).
【解析】
试题分析:(1)根据已知条件,易求得C、A的坐标,可用待定系数法求出抛物线的解析式;
(2)根据以点A、C、E、F为顶点的四边形为平行四边形,由平行四边形的性质以及二次函数的性质得出AE=CF,AE∥CF即可得出答案.
(3)易求得AC的长,由于AC长为定值,当P到直线AG的距离最大时,△APG的面积最大.可过P作y轴的平行线,交AG于Q;设出P点坐标,根据直线AG的解析式可求出Q点坐标,也就求出PQ的长,进而可得出关于△APG的面积与P点坐标的函数关系式,根据函数的性质可求出△APG的最大面积及P点的坐标,根据此时△APG的面积和AG的长,即可求出P到直线AC的最大距离.
试题解析:(1)由已知得:C(0,-3),
设该表达式为: y=ax2+bx+c=a(x+1)(x-3)
将C点的坐标代入得:a=1
所以这个二次函数的表达式为:y=x2-2x-3;
(2)如图,

又y=(x-1)2-4,∴顶点D(1,-4).
容易求得直线CD的表达式是y=-x-3.
在y=-x-3中,令y=0,得x=-3.
∴E(-3,0),
∵A(-1,0),
∴AE=2.
在y=x2-2x-3中,令y=-3,得x1=0,x2=2,
∴CF=2,
∴AE=CF.
∵AE∥CF,
∴四边形AECF为平行四边形,此时F(2,-3).
(3)过点P作y轴的平行线与AG交于点Q,
易得G(2,-3),直线AG为y=-x-1;
设P(x,x2-2x-3),则Q(x,-x-1),PQ=-x2+x+2;
S△APG=S△APQ+S△GPQ= (?x2+x+2)×3=?
(?x2+x+2)×3=? (x?
(x? )2+
)2+
当x= 时,△APG的面积最大为
时,△APG的面积最大为 ;
;
又AG=3 ,P到AG的最大距离为
,P到AG的最大距离为 =
= =
= ,此时P点的坐标为(
,此时P点的坐标为( ,-
,- ).
).

考点:1、待定系数法;2、平行四边形的判定;3、图形的面积


科目:初中数学 来源:2014-2015学年浙江省嘉兴市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为 cm,则弦CD的长为( )
cm,则弦CD的长为( )

A. B.3cm C.
B.3cm C. D.9cm
D.9cm
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省宁波市九年级10月月考数学试卷(解析版) 题型:解答题
(本题满分8分)如图,已知反比例函数 与一次函数
与一次函数 的图象在第一象限相交于点A(1,
的图象在第一象限相交于点A(1, )
)

(1)试确定这两个函数的表达式;
(2)求出这两个函数图像的另一个交点B的坐标,并根据图象写出使一次函数的值小于反比例函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省宁波市部九年级上学期第一次月考数学试卷(解析版) 题型:解答题
已知二次函数y=x2-mx+m-2:
(1)求证:不论m为任何实数,此二次函数的图象与x轴都有两个交点;
(2)当二次函数的图象经过点(3,6)时,确定m的值,并写出此二次函数与坐标轴的交点坐标。.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省嘉兴市实验学校九年级上学期期中考试数学试卷(解析版) 题型:填空题
当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省嘉兴市八年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,△ABE≌△ACD,∠ADB=105°,∠B=60°则∠BAE= .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省富阳市共同体九年级10月月考数学试卷(解析版) 题型:选择题
二次函数 的图象的对称轴是( )
的图象的对称轴是( )
A.直线 =-2 B.直线
=-2 B.直线 =2 C.直线
=2 C.直线 =-1 D.直线
=-1 D.直线 =1
=1
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省联盟七年级上学期期中数学试卷(解析版) 题型:解答题
(本题10分)司机在驾驶汽车时,发现紧急情况到踩下刹车需要一段时间,这段时间叫反应时间,之后还会继续行驶一段距离.我们把司机从发现紧急情况到汽车停止所行驶的这段距离叫“刹车距离”(如图).

已知汽车的刹车距离 (单位:米)与车速
(单位:米)与车速 (单位:米/秒)之间有如下关系:
(单位:米/秒)之间有如下关系: ,其中
,其中 为司机的反应时间(单位:秒),
为司机的反应时间(单位:秒), 为制动系数.某机构为测试司机饮酒后刹车距离的变化,对某种型号的汽车进行了“醉汉”驾车测试,已知该型号汽车的制动系数
为制动系数.某机构为测试司机饮酒后刹车距离的变化,对某种型号的汽车进行了“醉汉”驾车测试,已知该型号汽车的制动系数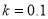 ,并测得志愿者在未饮酒时的反应时间
,并测得志愿者在未饮酒时的反应时间 秒.
秒.
(1)若志愿者未饮酒,且车速为10米/秒,则该汽车的刹车距离为 米 ;
(2)当志愿者在喝下一瓶啤酒半小时后,以15米/秒的速度驾车行驶,测得刹车距离为52.5米,此时该志愿者的反应时间是 秒.
(3)假如该志愿者当初是以10米/秒的车速行驶,则刹车距离将比未饮酒时增加多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com