Question

已知二次函数y=x2-mx+m-2：

（1）求证：不论m为任何实数，此二次函数的图象与x轴都有两个交点；

（2）当二次函数的图象经过点（3，6）时，确定m的值，并写出此二次函数与坐标轴的交点坐标。．

 

Answer 1

（1）证明见解析；

（2）m=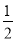；二次函数与坐标轴的交点坐标分别为（0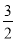，-）、（-1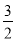，0）、（，0）；

【解析】

试题分析：（1）先计算根的判别式，然后判断根的判别式的值是否大于0即可得证；

（2）将点（3，6）代入解析式即可求得m的值，然后分别令x=0、y=0即可得到二次函数与坐标轴的交点坐标；

试题解析：（1）∵△=（-m）2-4（m-2）=m2-4m+8=（m-2）2+4

不论m为任何实数，（m-2）2≥0

∴（m-2）2+4≥4>0

即△>0

∴二次函数的图象与x轴都有两个交点；

（2）将点（3，6）代入得6=9-3m+m-2,解得m=；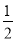

所以二次函数的解析式为y=x2-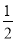x-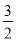，令x=0，则y=-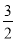；令y=0,则x1=-1，x2=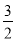；所以二次函数与坐标轴的交点坐标分别为（0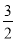，-）、（-1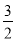，0）、（，0）；

考点：1、二次函数与坐标轴的交点特征；2、根的判别式；3、待定系数法