
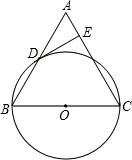
 已知,如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
已知,如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.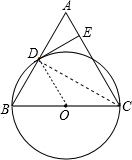 (1)证明:连结CD,如图,
(1)证明:连结CD,如图,

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、5 | B、8 |
| C、-11 | D、5或-11 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 在数学课外实践活动中,小于在一条河西岸一段上的A,B两点处利用测角仪分别对东岸的C点进行测量,测得BC与河西岸夹角60°,AC与河西岸夹角75°,且AB=100米,求点C到河西岸的距离.(精确到1米,tan60°≈1.73,tan75°≈3.73)
在数学课外实践活动中,小于在一条河西岸一段上的A,B两点处利用测角仪分别对东岸的C点进行测量,测得BC与河西岸夹角60°,AC与河西岸夹角75°,且AB=100米,求点C到河西岸的距离.(精确到1米,tan60°≈1.73,tan75°≈3.73)查看答案和解析>>
科目:初中数学 来源: 题型:
 在物理试验中,当电流在一定时间段内正常通过电子元件
在物理试验中,当电流在一定时间段内正常通过电子元件 时,每个电子元件的状态有两种可能:通电或断开,并且这两种状态的可能性相等.当有两个电子元件a、b并联时,P、Q之间电流通过的概率是
时,每个电子元件的状态有两种可能:通电或断开,并且这两种状态的可能性相等.当有两个电子元件a、b并联时,P、Q之间电流通过的概率是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com