
 在数学课外实践活动中,小于在一条河西岸一段上的A,B两点处利用测角仪分别对东岸的C点进行测量,测得BC与河西岸夹角60°,AC与河西岸夹角75°,且AB=100米,求点C到河西岸的距离.(精确到1米,tan60°≈1.73,tan75°≈3.73)
在数学课外实践活动中,小于在一条河西岸一段上的A,B两点处利用测角仪分别对东岸的C点进行测量,测得BC与河西岸夹角60°,AC与河西岸夹角75°,且AB=100米,求点C到河西岸的距离.(精确到1米,tan60°≈1.73,tan75°≈3.73)| EC |
| tan60° |
| EC |
| tan75° |
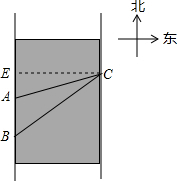 解:如图,过点C作CE⊥AB于点E.
解:如图,过点C作CE⊥AB于点E.| CE |
| BE |
| CE |
| tan60° |
| EC |
| tan75° |
| CE |
| tan60° |
| EC |
| tan75° |
| 100×tan60°×tan75° |
| tan75°-tan60° |
| 100×1.73×1.73 |
| 3.73-1.73 |


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
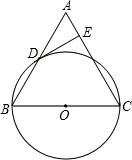 已知,如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
已知,如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com