练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
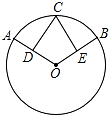
    如图，D、E分别是半径OA和OB的中点，
    AC
    =
    CB
    ，CD与CE的大小有什么关系？试说明你的理由．
    考点：圆心角、弧、弦的关系,全等三角形的判定与性质
    专题：
    分析：求出OD=OE，∠DOC=∠EOC，根据SAS推出△DOC≌△EOC，根据全等三角形的性质得出即可．
    解答：解：CD=CE，
    理由是：连接OC，
    ∵D、E分别是半径OA和OB的中点，
    ∴OD=OE，
    ∵
    AC
    =
    CB
    ，
    ∴∠DOC=∠EOC，
    在△DOC和△EOC中，
    OC=OC
    ∠DOC=∠EOC
    OD=OE
    ，
    ∴△DOC≌△EOC（SAS），
    ∴CD=CE．
    点评：本题考查了全等三角形的性质和判定，圆心角、弧、弦之间的关系的应用，解此题的关键是正确作出辅助线后求出△DOC≌△EOC，难度适中．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    含有字母x，y且系数为1的三次单项式有
     
    个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算|-5|-5的结果是（　　）
    A、0B、-5C、10D、-10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在元旦联欢会上，有一个开盒有奖的游戏，两只外观一样的盒子，一只装有奖品，一只是空的，游戏规定：每人每次游戏时主持人先混合盒子再拿出来，参加游戏的同学随机打开其中一只，若有奖品，就获得该奖品，若是空盒子，就表演一个节目．
    （1）两个人参加游戏，都获奖的概率为
     
    ．
    （2）n个人参加游戏，全部获奖的概率为
     
    ．
    （3）现取三只外观一样的盒子，一只内有奖品，另两只空盒子，游戏规则不变．两个人参加游戏，用画树形图法求至少有一个人表演节目的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在边长为1的小正方形组成的正方形网格中建立如图片所示的平面直角坐标系，已知格点三角形ABC（三角形的三个顶点都在小正方形上）
    （1）画出△ABC关于直线l：x=-1的对称三角形△A1B1C1；并写出A1、B1、C1的坐标．
    （2）在直线x=-l上找一点D，使BD+CD最小，满足条件的D点为
     
    ．
    提示：直线x=-l是过点（-1，0）且垂直于x轴的直线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

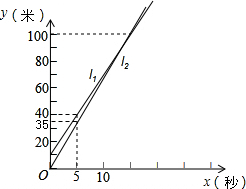    小明和小亮进行百米赛跑，小明比小亮跑得快，如果两人同时起跑，小明肯定赢，现在小明让小亮先跑若干米，两人的路程y（米）分别与小明追赶时间x（秒）的函数关系如图所示．
    （1）小明让小亮先跑了多少米？
    （2）分别求出表示小明、小亮的路程与时间的函数关系式．
    （3）谁将赢得这场比赛？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在△ABC中，AB=3，BC=
    		3
    ，∠A=30°，则△ABC的面积为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，已知两个同心圆中，大圆的弦AB、AC切小圆于D、E，△ABC的周长为16cm，求△ADE的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在数学课外实践活动中，小于在一条河西岸一段上的A，B两点处利用测角仪分别对东岸的C点进行测量，测得BC与河西岸夹角60°，AC与河西岸夹角75°，且AB=100米，求点C到河西岸的距离．（精确到1米，tan60°≈1.73，tan75°≈3.73）

    查看答案和解析>>

    同步练习册答案