【题目】如图所示的网格是正方形网格，则
__________
（点
，
，
，
，
是网格线交点）．
【答案】
【解析】
连接CG、AG,根据勾股定理的逆定理可得∠CAG=90°,从而知△CAG是等腰直角三角形,根据平行线的性质和三角形全等,可知,∠BAC-∠DAE=∠ACG,即可得解．
解:如图,连接CG、AG,
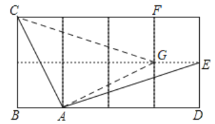
由勾股定理得:AC2=AG2=12+22=5，CG2=12+32=10,
∴AC2+AG2=CG2,
∴∠CAG=90°,
∴△CAG是等腰直角三角形,
∴∠ACG=45°,
∵CF∥AB,
∴∠ACF=∠BAC,
在△CFG和△ADE中,
∵CF＝AD, ∠CFG＝∠ADE＝90°, FG＝DE,
∴△CFG≌△ADE（SAS）,
∴∠FCG=∠DAE,
∴∠BAC-∠DAE=∠ACF-∠FCG=∠ACG=45°,
故答案为：45．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】已知x1，x2是关于x的一元二次方程
的两实数根．
（1）求m的范围；
（2）若
，求m的值；
（3）已知等腰△ABC的一边长为7，若x1，x2恰好是△ABC另外两边的边长，求这个三角形的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
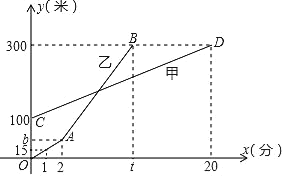
【题目】甲、乙两人相约周末登花果山，甲、乙两人距地面的高度y（米）与登山时间x（分）之间的函数图象如图所示，根据图象所提供的信息解答下列问题：
（1）甲登山上升的速度是每分钟 米，乙在A地时距地面的高度b为 米；
（2）若乙提速后，乙的登山上升速度是甲登山上升速度的3倍，请求出乙登山全程中，距地面的高度y（米）与登山时间x（分）之间的函数关系式；
（3）登山多长时间时，甲、乙两人距地面的高度差为70米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，一次函数
的图象交
轴、
轴分别于
两点，交直线
于
。
（1）求点的坐标；
（2）若
，求
的值；
（3）在（2）的条件下，
是线段
上一点，
轴于
，交
于
，若
，求点的坐标。
查看答案和解析>>
科目：初中数学 来源： 题型：
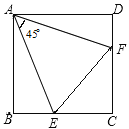
【题目】如图，在正方形ABCD中，点E在BC上，点F在CD上，连接AE、AF、EF，∠EAF=45°，BE=3，CF=4，则正方形的边长为__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
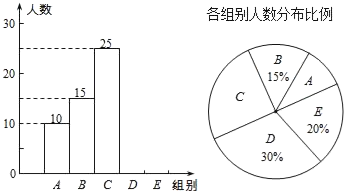
【题目】某校举行全体学生“汉字听写”比赛，每位学生听写汉字39个．随机抽取了部分学生的听写结果，绘制成如下的图表．
组别 | 正确字数x | 人数 |
A | 0≤x＜8 | 10 |
B | 8≤x＜16 | 15 |
C | 16≤x＜24 | 25 |
D | 24≤x＜32 | m |
E | 32≤x＜40 | n |
根据以上信息完成下列问题：
（1）统计表中的m＝ ，n＝ ，并补全条形统计图；
（2）扇形统计图中“C组”所对应的圆心角的度数是 ；
（3）已知该校共有900名学生，如果听写正确的字的个数少于24个定为不合格，请你估计该校本次听写比赛不合格的学生人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】操作：在△ABC中，AC＝BC＝2，∠C＝90°，将一块等腰三角形板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点。图①，②，③是旋转三角板得到的图形中的3种情况。研究：
（1）三角板ABC绕点P旋转，观察线段PD和PE之间有什么数量关系？并结合图②加以证明。
（2）三角板ABC绕点P旋转，△PBE是否能为等腰三角形？若能，指出所有情况（即写出△PBE为等腰三角形时CE的长）；若不能，请说明理由。（图④不用）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，阳光下，小亮的身高如图中线段AB所示，他在地面上的影子如图中线段BC所示，线段DE表示旗杆的高，线段FG表示一堵高墙．
（1）请你在图中画出旗杆在同一时刻阳光照射下形成的影子，并用线段表示；
（2）如果小亮的身高AB=1.6m，他的影子BC=2.4m，旗杆的高DE=15m，旗杆与高墙的距离EG=16m，请求出旗杆的影子落在墙上的长度．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
