
【题目】操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角形板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点。图①,②,③是旋转三角板得到的图形中的3种情况。研究:
(1)三角板ABC绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合图②加以证明。
(2)三角板ABC绕点P旋转,△PBE是否能为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由。(图④不用)

【答案】(1)PD=PE;(2)CE=0或1.
【解析】
试题分析:连接PC,根据题意得出CP=PB,∠ACP=∠B=45°,∠DPC=∠BPE,从而得出△PCD和△PBE全等,从得出答案;第二题分PE=PB,PB=BE和PE=BE三种情况分别进行讨论.
试题解析:(1)由图①可猜想PD=PE,再在图②中构造全等三角形来说明.即PD=PE.
理由如下:连接PC,因为△ABC是等腰直角三角形,P是AB的中点,∴CP=PB,CP⊥AB,∠ACP= ∠ACB=45°.
∴∠ACP=∠B=45°.又∠DPC+∠CPE=∠BPE+∠CPE,∴∠DPC=∠BPE.
∴△PCD≌△PBE. ∴PD=PE.
(2)△PBE是等腰三角形,
①当PE=PB时,此时点C与点E重合,CE=0;
②当PB=BE时,1)E在线段BC上, ,2)E在CB的延长线上,
③当PE=BE时,CE=1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线 AC、BD 相交成的锐角α=30°,若 AC=8,BD=6,则□ABCD的面积是( )
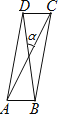
A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与操作:一般地,如果把一个图形绕着一个定点旋转一定角度α(α小于360°)后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对称中心,α叫做这个旋转对称图形的一个旋转角,请根据上述规定解答下列问题:
(1)请写出一个有一个旋转角是90°旋转对称图形,这个图形可以是_____;
(2)尺规作图:在图中的等边三角形内部作出一个图形,使作出的图形和这个等边三角形构成的整体既是一个旋转对称图形又是一个轴对称图形(作出的图形用实线,作图过程用虚线,保留痕迹,不写做法).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第12个图形中有全等三角形的对数是( )
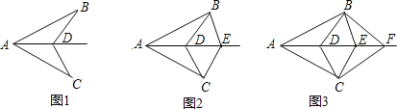
A. 80对B. 78对C. 76对D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC中,D为边AC上一点.
(1)以BD为边作等边△BDE,连接CE,求证:AD=CE;
(2)如果以BD为斜边作Rt△BDE,且∠BDE=30°,连接CE并延长,与AB的延长线交于F点,求证:AD=BF;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般的,数a的绝对值|a|表示数a对应的点与原点的距离.同理,绝对值|a﹣b|表示数轴上数a对应的点与数b对应的点的距离.例如:|3﹣0|指在数轴上表示数3的点与原点的距离,所以3的绝对值是3,即|3﹣0|=|3|=3.|6﹣2|指数轴上表示6的点和表示2的点的距离,所以数轴上表示6的点和表示2的点的距离是4,即|6﹣2|=4.
结合数轴与绝对值的知识解答下列问题:
(1)解含绝对值的方程|x+2|=1得x的解为 ;
(2)解含绝对值的不等式|x+5|<3得x的取值范围是 ;
(3)求含绝对值的方程![]() 的整数解;
的整数解;
(4)解含绝对值的不等式|x﹣1|+|x﹣2|>4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12 m,由此他就知道了A,B间的距离,有关他这次探究活动的描述错误的是( )
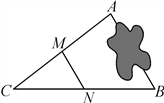
A. AB=24 m B. MN∥AB C. △CMN∽△CAB D. CM∶MA=1∶2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com