
【题目】如图,已知等边△ABC中,D为边AC上一点.
(1)以BD为边作等边△BDE,连接CE,求证:AD=CE;
(2)如果以BD为斜边作Rt△BDE,且∠BDE=30°,连接CE并延长,与AB的延长线交于F点,求证:AD=BF;

【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)欲证明AD=CE,只要证明△ABD≌△CBE即可;
(2)如图2中,倍长BE到H,连CH,DH.首先证明△DBH是等边三角形,由(1)可知,△ABD≌△CBH,推出AD=CH,∠A=∠HCB=∠ABC=60°,推出BF∥CH,推出∠F=∠ECH,再证明△EBF≌△EHC,推出BF=CH,由此即可证明.
(1)证明:如图1中,
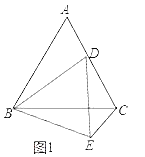
∵△ABC,△BDE都是等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABD=∠CBE,
在△ABD和△CBE中, 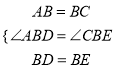 ,
,
∴△ABD≌△CBE,
∴AD=CE.
(2)如图2中,倍长BE到H,连CH,DH.
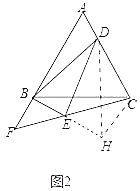
∵BE=EH,DE⊥BH,
∴DB=DH,∠BDE=∠HDE=30°,
∴∠BDH=60°,
∴△DBH是等边三角形,
由(1)可知,△ABD≌△CBH,
∴AD=CH,∠A=∠HCB=∠ABC=60°,
∴BF∥CH,
∴∠F=∠ECH,
在△EBF和△EHC中, 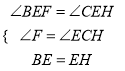 ,
,
∴△EBF≌△EHC,
∴BF=CH,
∴AD=CE.


科目:初中数学 来源: 题型:
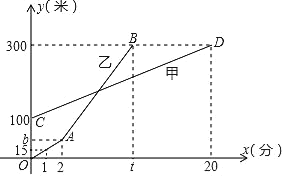
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
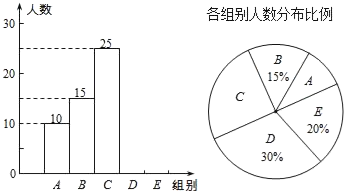
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角形板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点。图①,②,③是旋转三角板得到的图形中的3种情况。研究:
(1)三角板ABC绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合图②加以证明。
(2)三角板ABC绕点P旋转,△PBE是否能为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由。(图④不用)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委为积极参与“陶行知杯.全国书法大赛”现场决赛,向学校学生征集书画作品,今年3月份举行了“书画比赛”初赛,初赛成绩评定为A,B,C,D,E五个等级.该校七年级书法班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题.

(1)该校七年级书法班共有 名学生;扇形统计图中C等级所对应扇形的圆心角等于 度,并补全条形统计图;
(2)A等级的4名学生中有2名男生,2名女生,现从中任意选取2名学生参加“陶行知杯.全国书法大赛”现场决赛,请你用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数![]() ,导致了第一次数学危机.
,导致了第一次数学危机.![]() 是无理数的证明如下:
是无理数的证明如下:
假设![]() 是有理数,那么它可以表示成
是有理数,那么它可以表示成![]() (
(![]() 与
与![]() 是互质的两个正整数).于是
是互质的两个正整数).于是 ,所以,
,所以,![]() .于是
.于是![]() 是偶数,进而
是偶数,进而![]() 是偶数.从而可设
是偶数.从而可设![]() ,所以
,所以![]() ,
,![]() ,于是可得
,于是可得![]() 也是偶数.这与“
也是偶数.这与“![]() 与
与![]() 是互质的两个正整数”矛盾,从而可知“
是互质的两个正整数”矛盾,从而可知“![]() 是有理数”的假设不成立,所以,
是有理数”的假设不成立,所以,![]() 是无理数.这种证明“
是无理数.这种证明“![]() 是无理数”的方法是( )
是无理数”的方法是( )
A.综合法B.反证法C.举反例法D.数学归纳法
查看答案和解析>>
科目:初中数学 来源: 题型:
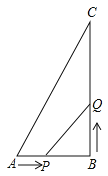
【题目】如图,在直角三角形![]() 中,
中,![]() ,点
,点![]() 从
从![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.
的速度移动. ![]() 分别从
分别从![]() 同时出发,当一个动点到达终点则另一动点也随之停止运动,
同时出发,当一个动点到达终点则另一动点也随之停止运动,
(1)求![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
(2)是否存在某一时刻![]() ,使点
,使点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
(3)点![]() 在运动的过程中,是否存在某时刻
在运动的过程中,是否存在某时刻![]() , 直线
, 直线![]() 把
把![]() 的周长分为
的周长分为![]() 两部分?若存在,求出
两部分?若存在,求出![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子,并用线段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
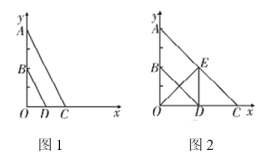
【题目】如图,平面直角坐标系中,![]() ,
,![]() ,点
,点![]() 是
是![]() 轴上点,点
轴上点,点![]() 为
为![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)若点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() 与
与![]() 的距离等于
的距离等于![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图2,若点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() 于点
于点![]() ,当四边形
,当四边形![]() 为平行四边形时,求直线
为平行四边形时,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com