
【题目】公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数![]() ,导致了第一次数学危机.
,导致了第一次数学危机.![]() 是无理数的证明如下:
是无理数的证明如下:
假设![]() 是有理数,那么它可以表示成
是有理数,那么它可以表示成![]() (
(![]() 与
与![]() 是互质的两个正整数).于是
是互质的两个正整数).于是 ,所以,
,所以,![]() .于是
.于是![]() 是偶数,进而
是偶数,进而![]() 是偶数.从而可设
是偶数.从而可设![]() ,所以
,所以![]() ,
,![]() ,于是可得
,于是可得![]() 也是偶数.这与“
也是偶数.这与“![]() 与
与![]() 是互质的两个正整数”矛盾,从而可知“
是互质的两个正整数”矛盾,从而可知“![]() 是有理数”的假设不成立,所以,
是有理数”的假设不成立,所以,![]() 是无理数.这种证明“
是无理数.这种证明“![]() 是无理数”的方法是( )
是无理数”的方法是( )
A.综合法B.反证法C.举反例法D.数学归纳法
科目:初中数学 来源: 题型:
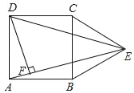
【题目】如图,在正方形ABCD的外侧,作等边三角形BCE,连接AE,DE.
(1)求证:AE=DE
(2)过点D作DF⊥AE,垂足为F,若AB=2cm,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与操作:一般地,如果把一个图形绕着一个定点旋转一定角度α(α小于360°)后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对称中心,α叫做这个旋转对称图形的一个旋转角,请根据上述规定解答下列问题:
(1)请写出一个有一个旋转角是90°旋转对称图形,这个图形可以是_____;
(2)尺规作图:在图中的等边三角形内部作出一个图形,使作出的图形和这个等边三角形构成的整体既是一个旋转对称图形又是一个轴对称图形(作出的图形用实线,作图过程用虚线,保留痕迹,不写做法).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第12个图形中有全等三角形的对数是( )
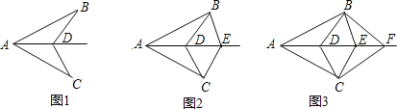
A. 80对B. 78对C. 76对D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC中,D为边AC上一点.
(1)以BD为边作等边△BDE,连接CE,求证:AD=CE;
(2)如果以BD为斜边作Rt△BDE,且∠BDE=30°,连接CE并延长,与AB的延长线交于F点,求证:AD=BF;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校综合实践活动小组的同学为了解七年级学生上学期参加综合实践活动的情况,随机抽样调查了学校部分七年级学生一个学期参加综合实践活动的情况,并用得到的数据绘制了下面两幅不完整的统计图.

根据统计图中的信息解决问题:
(1)扇形统计图中的a= ,并把条形统计图补充完整;
(2)对于“综合实践活动为6天”的扇形,对应的圆心角为 度;
(3)如果全市七年级共有12000名学生,通过计算说明“综合实践活动不超过4天”的有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般的,数a的绝对值|a|表示数a对应的点与原点的距离.同理,绝对值|a﹣b|表示数轴上数a对应的点与数b对应的点的距离.例如:|3﹣0|指在数轴上表示数3的点与原点的距离,所以3的绝对值是3,即|3﹣0|=|3|=3.|6﹣2|指数轴上表示6的点和表示2的点的距离,所以数轴上表示6的点和表示2的点的距离是4,即|6﹣2|=4.
结合数轴与绝对值的知识解答下列问题:
(1)解含绝对值的方程|x+2|=1得x的解为 ;
(2)解含绝对值的不等式|x+5|<3得x的取值范围是 ;
(3)求含绝对值的方程![]() 的整数解;
的整数解;
(4)解含绝对值的不等式|x﹣1|+|x﹣2|>4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,点
,点![]() .
.
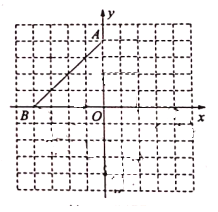
(1)①画出线段![]() 关于
关于![]() 轴对称的线段
轴对称的线段![]() ,则点
,则点![]() 的坐标为 ;
的坐标为 ;
②将线段![]() 平移至
平移至![]() ,其中点
,其中点![]() 与点
与点![]() 对应,画出线段
对应,画出线段![]() 并写出点
并写出点![]() 的坐标;
的坐标;
(2)点![]() 在(1)中四边形
在(1)中四边形![]() 边
边![]() 上,且
上,且![]() 是对角线
是对角线![]() 上--动点,则
上--动点,则![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com